二维数组内存分析

二维数组的逻辑结构是按行列排列的，但实际上二维数组在内存中还是占据一块连续的内存空间，其排列也是线性的，只是编译器在解读二维数组时会按照指定的行列去解读二维数组。

定义一个2行3列的二维数组，示例代码如下：

int arr[2][3]={{1,2,3},{4,5,6}};

上述代码中，arr是二维数组的数组名，该数组中包含两行数据，分别为{1,2,3}和{4,5,6}。从其形式上可以看出，这两行数据又分别为一个一维数组，所以二维数组又可视为数组元素为一维数组的一维数组。二维数组arr的逻辑结构与内存图解如图1所示。

图1 二维数组的逻辑结构与内存图解

由图1(c)可知，与一维数组一样，二维数组在内存中也是线性存储的。二维数组名是数组的起始地址，同时也是第1行元素的首地址和第1个元素的地址。但与一维数组名不同的是，二维数组名是一个二级指针，对二维数组名执行取值运算，其结果还是一个地址，这个地址与数组起始地址相同，对数组名执行两次取值操作才可以取到第1个元素。示例代码如下：

printf("arr:%p\n", arr);        //数组起始地址
printf("*arr:%p\n", *arr);       //数组起始地址
printf("**arr:%d\n", **arr);      //执行两次取值运算，取到数组首元素
printf("arr[0]:%p\n", arr[0]);     //数组起始地址
printf("arr[0][0]:%d\n", arr[0][0]);  //数组首元素
printf("&arr[0][0]:%p\n", &arr[0][0]); //数组起始地址

要理解二维数组起始地址、首行地址、首元素地址之间的关系。这里首先将二维数组arr看作是元素是arr[0]、arr[1]的一维数组，数组名arr与各数组元素之间的关系如下：

● 将arr看作一维数组，arr就是该一维数组的数组名，代表该一维数组的首元素地址，即第一个元素arr[0]的地址。

● 表达式arr+1表示第2个元素的地址，即arr[1]的地址。

其次，将arr[0]、arr[1]两个元素分别看成是由3个int类型元素组成的一维数组。数组arr[0]与各数组元素之间的关系如下：

● arr[0]是一维数组的数组名，代表该一维数组的首元素地址，即第一个元素arr[0][0]的地址。

● 表达式arr[0]+1代表下一个元素arr[0][1]的地址。

● 表达式arr[0]+2代表arr[0][2]的地址。

数组arr的行地址与列地址之间的关系如图2所示。

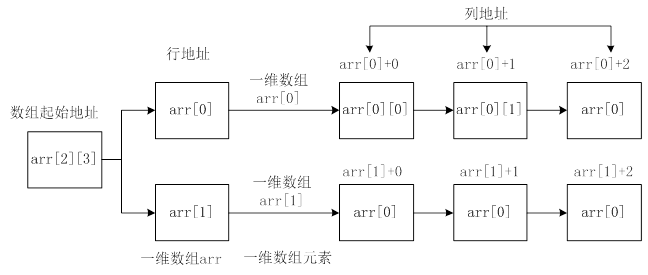
图2 数组arr的行地址与列地址示意图

根据上面的分析，可推导出如下结论：

● arr[i]（即*(arr+i)）可以看成是一维数组arr的索引为i的元素，同时又可以看成是由arr[i][0]、arr[i][1]、arr[i][2]等元素组成的一维数组的数组名，代表这个一维数组的首元素地址，即第一个元素arr[i][0]的地址；

● arr[i]+j（即*(arr+i)+j）代表这个数组中索引为j的元素的地址，即arr[i][j]的地址；

●** (arr[i]+j)即((arr+i)+j)就代表这个地址所指向的元素的值，即数组索引为j的元素arr[i][j]的值。**

因此，下面表示元素arr[i][j]的5种形式是等价的：

arr[i][j]
*(arr[i]+j)
*(*(arr+i)+j)
(*(arr+i))[j]
*(*(arr+i)[j])

二维数组数组名与第1行地址相同，即arr的值与arr[0]的值相同，按照这个逻辑思路，二维数组名arr+0表示第1行地址，则arr+i代表二维数组arr的第i+1行的地址；arr[0]+0可看成第1行第1列地址，那么arr[i]+j就表示第i+1行第j+1列的地址。行地址arr每次加1，表示指向下一行，列地址arr[i]每次加1，表示指向下一列，即该行的下一个元素。经过上述分析，可按如下方式理解表达式“((arr+i)+j)”的含义：

arr       // 第1行的地址
arr+i      // 第（i+1）行的地址
*(arr+i)    // 即arr[i],第（i+1）行第1列的地址
*(arr+i)+j   // 即&arr[i][j],数组arr[i]的第（j+1）列的地址
*(*(arr+i)+j)  // 即arr[i][j],数组arr[i]的第（j+1）列的元素

作个类比，二维数组的行地址好比一座旅馆的楼层号，列地址好比旅馆每一层的房间号，如果用编号0412代表该旅馆第4层门牌号12的话，那么要想找到这间房间，应该先上第4层楼，再在第4层楼上门牌号是12的房间。

在二维数组中，数组列步长与数组类型相同，在同一行中，相邻元素间的地址间距就是元素所占的内存大小，例如，在二维数组arr的第1行，元素arr[0][0]到元素arr[0][1]，步长是4个字节，即列索引每增加1，其步长是4个字节，是数据类型的大小。

数组行步长是数据类型大小与该行元素个数的乘积，从arr[0]到arr[1]跨越了一整行，如图6-24中的(b)和(c)，从元素1到元素4，其间跨越了3个元素，地址距离为12个字节，即数组arr的行步长为12字节。

这就相当于查找旅馆房间时，假如一层有20个房间，如果楼层号不变，那么相邻房间之间的距离是房间大小，但如果从4层到5层，则跨越了20个房间。

相对于一维数组，二维数组的逻辑存储形式稍显复杂，但只要掌握了数组的本质结构，学习起来会很容易。