栈的递归应用

所谓递归就是程序调用自身的过程，它可以把一个大型的、复杂的问题层层转化为一个与原问题相似的、规模较小的问题来求解，递归策略只需少量的代码就可描述出解题过程中所需要的多次重复计算，大大地减少了程序的代码量。

一般来说，递归需要有临界条件：递归前进和递归返回段。否则递归将无限调用，永远无法结束程序，最后会造成内存崩溃。

递归作为一种算法在程序设计语言中被广泛应用，例如，在数学运算中经常遇到计算自然数和的情况，假设要计算1~n之间自然数之和，就需要先计算1加2的结果，用这个结果加3再得到一个结果，用新得到的结果加4，以此类推，直到用1~(n-1)之间所有数的和加n。此题就可以用递归来解决，其具体实现如例1所示。

例1

 1    #define _CRT_SECURE_NO_WARNINGS
 2    #include <stdio.h>
 3    #include <stdlib.h>
 4    
 5    int getSum(int n)
 6    {
 7        if (n == 1)
 8            return 1;
 9        int temp = getSum(n - 1); //调用自身
 10        return temp + n; //返回总和
 11    }
 12    
 13    int main()
 14    {
 15        int sum;
 16        int n;
 17        printf("请输入n的值：\n");
 18        scanf("%d", &n);
 19        sum = getSum(n);
 20        printf("结果：%d\n",sum);
 21    
 22        system("pause");
 23        return 0;
 24    }

运行结果如图1所示。

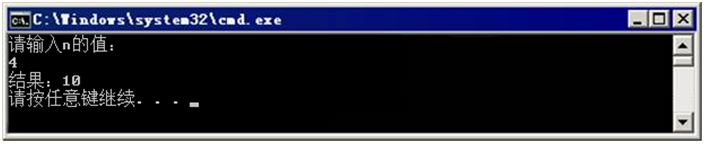
图1 例1运行结果

当输入4时，计算结果显示为10，是1-4的相加结果。由于函数的递归调用过程很复杂，此处通过一个图例来分析整个调用过程，如图2所示。

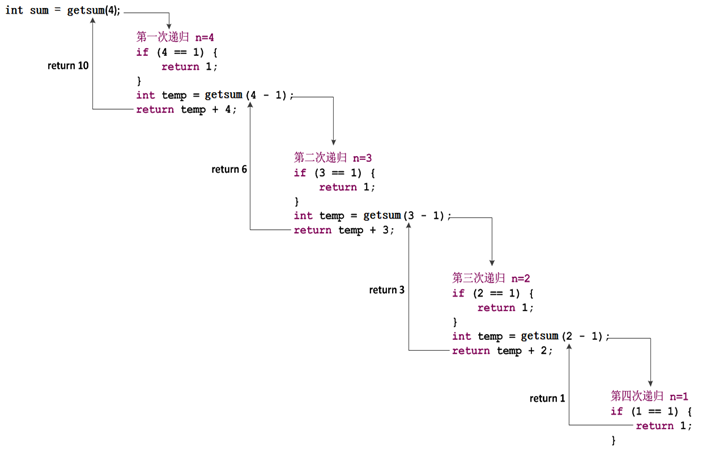
图2 递归调用过程

整个递归过程中getsum()函数被调用了4次，每次调用时，n的值都会减1。当n的值为1时，所有递归调用的函数都会以相反的顺序相继结束，所有的返回值会进行累加，最终得到的结果为10。

这样一个只有几步的递归过程，并不难理解，但读者可能会疑惑它与栈有何关系，接下来我们就来分析一下它在计算机中的运算过程。计算机在运行程序时都是用栈来存储程序中的变量、函数等，当定义了一个变量，变量入栈，使用完毕后就出栈。在递归运算时，函数也是不断的被调用进栈，当运行完毕后再依次出栈。接下来我们就分析一下例3-5中的递归调用过程。

（1）当传入参数n = 4时，调用getSum()函数，getSum()函数入栈，运行函数内代码，如图3所示。

图3 当n = 4时，函数入栈

（2）步骤（1）中再次调用getSum()函数，参数值为3，则getSum()再次入栈，如图4所示。

图4 当n = 3时，函数入栈

（3）步骤（2）中再一次调用了getSum()函数，参数值为2，则getSum()函数再次入栈……以此类推，直到n = 1时，getSum()函数最后一次入栈，此时栈中的情况如图5所示。

图5 getSum()函数进栈结束

（4）当n = 1时，返回值为1，返回给上次函数调用，则此次函数调用结束，函数出栈，如图6所示。

图7 n = 1时的函数调用弹出栈

（5）当n = 2，调用的函数得到出栈的函数返回的值时，就计算出了它这一步调用的结果，将结果返回后，本次调用结束，函数出栈，如图8所示。

图8 n = 2时的函数调用出栈

（6）依此类推，直到第一次函数调用（n = 4时）结束，将计算出的结果返回，然后弹栈， 如图9所示。

图9 所有函数调用都已弹栈

这就是递归在栈中实现的执行和回退过程，回退过程的顺序是执行过程的逆序，下一次调用都为上一次调用提供需求，显然这很符合栈的特点，编绎器就是利用这个特点来实现递归管理的。当然，对于现在的高级语言来说，这样的递归，以及程序中变量的管理是不需要程序员自己来操作的，一切都由操作系统执行，但读者也需要理解其原理。