用栈实现四则运算
我们都知道,计算机的基本功能大多都基于对数据的操作,给出一个运算式,计算机能迅速计算出其结果,若运算式有错误,例如运算式“1+3*(2+5”,右边少了一个“)”,编绎器会立刻检查出错误并报告,那么计算机是如何做到的呢?
其实计算机在进行运算时,将运算表达式转换成了逆波兰表达式,这是一种不需要括号的后缀表达方式,例如“1+2”经转换变为“1 2 +”,然后再进行计算。而在转换的过程中,这些数据就保存在栈中。需要进行计算时,利用栈先进后出的特点来进行字符的匹配检查,直到完成转换再对后缀表达式计算结果。
计算机在这个过程中执行了两步操作:
(1)将中缀表达式转换为后缀表达式。
(2)对后缀表达式计算。
这两步操作都用到了栈,下面先来学习执行这两步操作的基本原理。
1、中缀转后缀
将中缀表达式转换为后缀表达式的过程中,数据是用栈来存储的,在遍历中缀表达式时,遵循以下规则:
● 对于数字:直接输出。
● 对于符号:
左括号:进栈,不管栈中是否有元素。
运算符:若此时栈为空,直接进栈。
若栈中有元素,则与栈顶符号进行优先级比较:
若新符号优先级高,则新符号进栈(默认左括号优先级最低,直接入栈)。
若新符号优先级低,将栈顶符号弹出并输出,之后使新符号进栈。
右括号:不断将栈顶符号弹出并输出,直到匹配到左括号,再接着读取下一个符号;须注意,左右括号匹配完成即可,并不将其输出。
● 遍历结束:将栈中所有的符号弹出并输出。
下面以“1+3*(2+5)”为例来分析中缀转后缀的转换过程。
(1)遍历字符串,第一个读取到的字符是1,则对于数字直接输出,如图1所示。
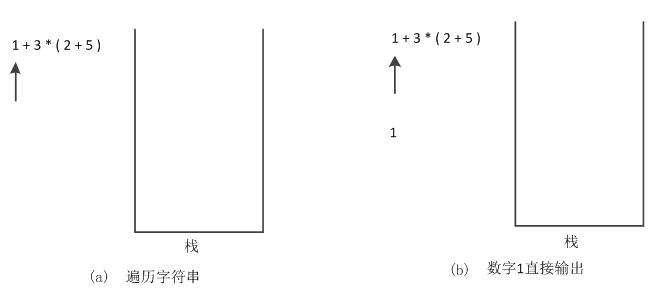
图1 遍历字符串
(2)数字1输出后,接着读取下一个字符,为符号“+”,是运算符,此时栈为空,直接进栈,如图2所示。
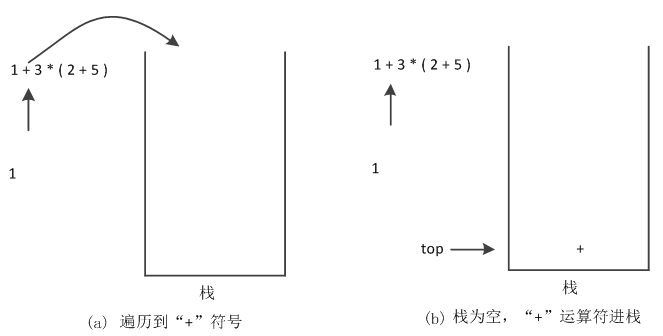
图2 “+”运算符进栈
(3)读取下一个字符, 为数字3,为数字,直接输出,如图3所示。
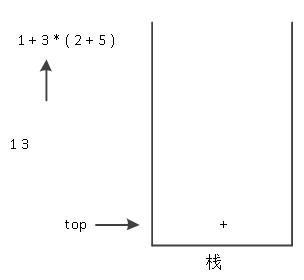
图3 数字3直接输出
(4)读取下一个字符,是符号“*”,与栈顶符号比较优先级,其优先级大于栈顶的“+”符号,进栈,如图4所示。
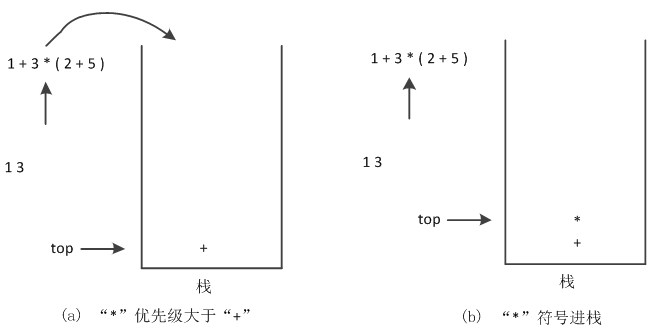
图4 “*”运算符进栈
(5)读取下一个字符,是“(”,“(”直接进栈,如图5所示。
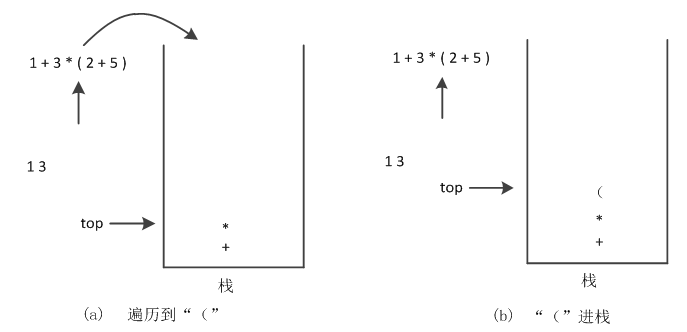
图5 “(”符号进栈
读取下一个字符,下一个字符为数字2,直接输出,如图6所示。

图6 数字2直接输出
(7)读取下一个字符,下一个字符为“+”,比较它与栈顶符号的优先级,因为“(”优先级默认最低,所以将新符号“+”号进栈,如图7所示。
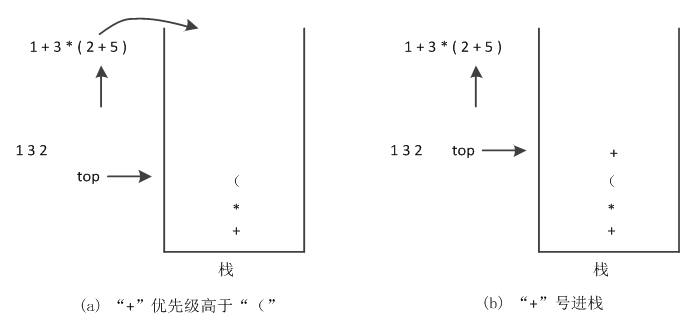
图7 “+”运算符进栈
(8)接着读取下一个字符,下一个字符是数字5,直接输出,如图8所示。
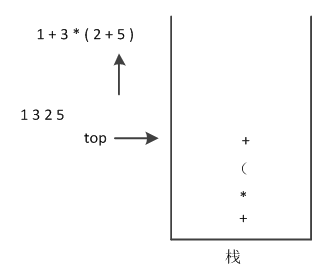
图8 数字5直接输出
(9)输出数字5后,接着读取下一个字符,下一个字符为“)”,则弹出栈顶符号并输出,直到匹配到“(”,如图9所示。
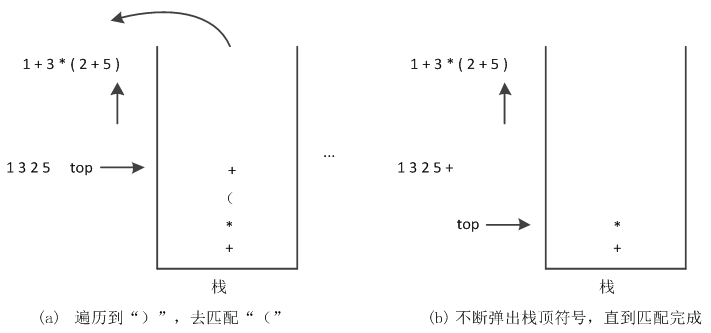
图9 遍历到“)”,匹配“(”
如果在输入表达式时少写了一左括号,那么在执行这一步时就会出错,因为将栈弹空也不会匹配到对应的左括号。
(10)左右括号匹配完成后,继续读取下一个字符,当遍历到下一个字符时,发现字符串已经遍历结束,则就将栈中的符号全部弹出并输出,其结果如图10所示。
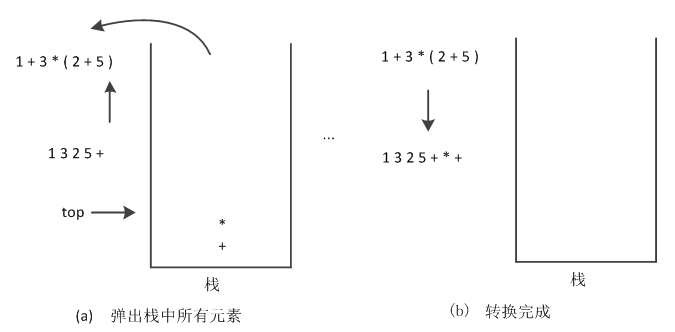
图10 转换完成
经过一系列的转换,中缀表达式“1+3(2+5)”转换为后缀表达式的结果为“1325++”,在这个转换匹配的过程中,如果有错误,例如在第(9)步过程中,如果运算式少写一个“(”左括号,则直到弹出栈中所有元素也匹配不到“(”符号,编绎器就会报错,像经常使用的头文件包含#include <stdio.h>等都是利用这个原理来检查的。
学习了上面的转换规则与过程,再结合上一节中学习过的栈,就可以通过编程来实现运算式的转换了。 在Visual Studio2013中创建一个项目,上一节中实现了一个链式栈,将头文件linkstack.h与函数实现文件linkstack.c添加进去,注意,在遍历运算式时是以字符串的形式进行的,因此需要将上一节栈的数据类型int改为char,修改后的结点定义如下:
struct Node //数据结点
{
char data; //数据,将int类型改为char
pNode next; //指针
};相应地,Push()函数的参数类型也要改为char,如下所示:
int Push(LinkStack lstack, char val); //插入元素类型为char其他的无须改动。在测试文件main.c中编写程序,具体如例1所示。
例1
main.c //测试文件
1 #define _CRT_SECURE_NO_WARNINGS
2 #include <stdio.h>
3 #include <stdlib.h>
4 #include "linkstack.h"
5
6 char buffer[256] = { 0 }; //临时缓冲区,从栈中弹出的元素可以先存放在这里
7 void Put(char ch)
8 {
9 static int index = 0;
10 buffer[index++] = ch; //将字符存入进来,然后索引index后移
11 }
12
13 //优先级比较函数
14 int Priority(char ch)
15 {
16 int ret = 0;
17 switch (ch)
18 {
19 case '+':
20 case '-':
21 ret = 1;
22 break;
23 case '*':
24 case '/':
25 ret = 2;
26 break;
27 default:
28 break;
29 }
30 return ret;
31 }
32
33 //判断字符是否是数字
34 int isNumber(char ch)
35 {
36 return (ch >= '0' && ch <= '9'); //是数字返回1,否则返回0
37 }
38
39 //判断字符是否是运算符
40 int isOperator(char ch)
41 {
42 return (ch == '+' || ch == '-' || ch == '*' || ch == '/');
43 }
44
45 //判断字符是否是左括号
46 int isLeft(char ch)
47 {
48 return (ch == '(');
49 }
50
51 //判断字符是否是右括号
52 int isRight(char ch)
53 {
54 return (ch == ')');
55 }
56
57 //函数功能:中缀转后缀表达式
58 //函数返回值:正确返回0;错误返回-1
59 int Transform(const char* str)
60 {
61 //在转换字符串时,先创建一个栈
62 LinkStack lstack = Create(); //创建栈
63
64 //创建完栈之后,就遍历字符串中的字符,数字输出,运算符入栈...
65 int i = 0;
66 while (str[i] != '\0')
67 {
68 //判断是否是数字
69 if (isNumber(str[i])) //如果是数字,就直接输出
70 {
71 Put(str[i]); //存入到buffer中
72 }
73 //判断是否是运算符
74 else if (isOperator(str[i]))
75 {
76 //如果是运算符,则先判断栈是否为空
77 if (!IsEmpty(lstack)) //如果栈不为空
78 {
79 //要比较此符号与栈顶符号的优先级
80 while (!IsEmpty(lstack)
81 &&Priority(*((char*)getTop(lstack)))
82 >= Priority(str[i]))
83 { //如果栈顶符号优先级高,就将栈顶符号弹出并输出
84 //直到栈顶符号的优先级
85 //小于此符号或者栈已弹空
86 Put(Pop(lstack)->data); //将弹出的栈顶符号存入到buffer中
87 }
88 }
89 Push(lstack, str[i]); //如果栈为空,符号直接入栈
90 }
91 //如果是左括号,直接入栈
92 else if (isLeft(str[i]))
93 {
94 Push(lstack, str[i]);
95 }
96 //如果是右括号
97 else if (isRight(str[i]))
98 {
99 //判断栈顶是不是左括号,如果不是,就弹出,直到匹配到左括号
100 while (!isLeft(*((char*)getTop(lstack))))
101 {
102 //弹出栈顶符号并存入到buffer中
103 Put(Pop(lstack)->data);
104 if (IsEmpty(lstack)) //如果弹出元素后,栈已经空了,就匹配错误
105 {
106 printf("没有匹配到左括号!\n");
107 return -1; //如果栈已为空,结束程序
108 }
109 }
110
111 Pop(lstack); //while循环结束,就匹配到了左括号
112 //将左括号弹出,注意不保存
113 }
114 else
115 {
116 printf("有不能识别字符!\n");
117 return -1;
118 }
119 i++;
120 }
121
122 //遍历结束后
123 if (str[i] == '\0')
124 {
125 //遍历结束后,将栈中所有符号依次弹出
126 while (!IsEmpty(lstack))
127 {
128 if (getTop(lstack)->data == '(') //如果栈中还有“(“,证明缺少右括号
129 {
130 printf("有没有匹配的“(”,缺少“)”\n");
131 return -1;
132 }
133 Put(Pop(lstack)->data);
134 }
135 }
136 else
137 {
138 printf("遍历没有完成!\n");
139 }
140 return 1;
141 }
142
143 int main()
144 {
145 char str[1024] = {0};//"1325+*+";
146 printf("请输入四则运算表达式:\n");
147 scanf("%s", str);
148
149 if(Transform(str) == -1)
150 printf("遍历中出现错误,无法完成转换!\n"); //转换
151 else
152 printf("转化后的表达式是: %s\n",buffer);
153 system("pause");
154 return 0;
155 }运行结果如图11所示。

图11 例1运行结果
由图11中的运行结果可知,当输入“1+3(2+5)”时,程序将其转换为了“1325++”,与图解分析的结果一致。再次运行,输入一个错误的表达式时,会出现出错提示,如图12所示。
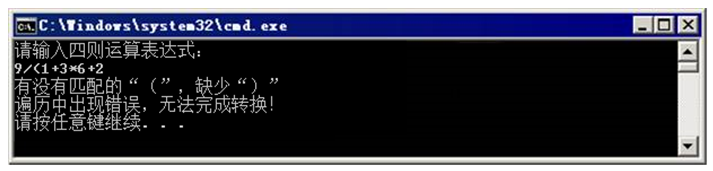
图12 例1错误表达式的运行结果
在例1中,代码第6行定义了一个全局的char类型数组buffer,用来临时存放要从栈中弹出的元素。整个转换过程中本段代码一共实现了七个函数。
代码7-11行的Put函数,将字符(即从栈中弹出的元素)存储到buffer中。
代码14-31行实现的Priority()函数,用来比较操作符的优先级。
代码34-37行实现的isNumber()函数,用来判断字符是否是数字的函数。
代码40-43行实现的isOperator()函数,用来判断字符是否是运算符的函数。
代码46-49行实现的isLeft()函数,用来判断字符是否是左括号的函数。
代码52-55行实现的isRight()函数,用来判断字符是否是右括号的函数。
代码59-138行是进行转换的核心,每遍历到一个字符就要调用相应函数判断是数字还是运算符,或者是左括号与右括号,以作不同的处理。
本例实现了简单的转换,做了一些容错处理。但它只能处理简单的一位数字的运算,如果是两位或多位数字,它并不能识别,例如“102+30”这样的表达式,虽然它转换后看起来并无异样,但它并没有按运算符来区分哪几位数是一个数字。
2、后缀表达式的运算
将中缀表达式转换为后缀表达式后,计算机会根据后缀表达式进行求值计算。计算过程中的数据也是存储在栈中,相对于中缀表达式转后缀表达式,,它对数字和运算符的处理相应要简单一些:
● 对于数字:进栈。
● 对于符号:
从栈中弹出右操作数;
从栈中弹出左操作数;
然后根据符号进行运算,将运算结果压入栈中。
● 遍历结束,栈中唯一数字就是运算结果。
以“1+3(2+5)”转换后的表达式“1325++”为例,分析其运算过程:
(1)遍历字符串,前几个字符都是数字,直接入栈,如图13所示。
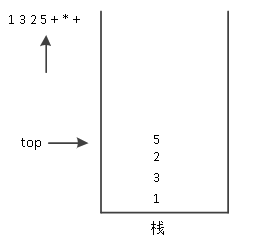
图13 数字入栈
(2)接着读取下一个字符,下一个字符是“+”号,则从栈中弹出右操作数与左操作数,进行运算,如图14所示。
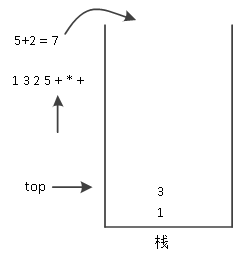
图14 左右操作数进行运算
(3)将运算结果压入栈中,如图15所示。
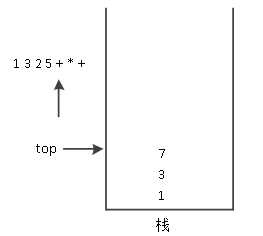
图16 运算结果7入栈
(4)运算结果入栈后,读取下一个字符,下一个字符为“”,弹出“”号的右与左两个操作数进行运算,然后将运算结果压入栈中,如图17所示。
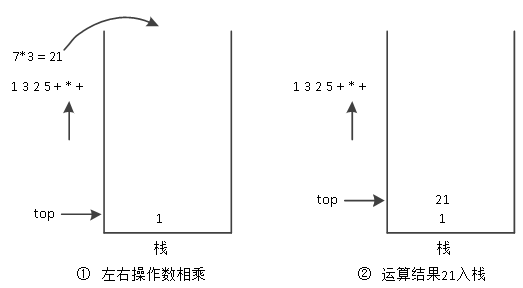
图17 运算结果21入栈
(5)运算结果21入栈后,再往下读取下一个字符,下一个字符为“+”运算符,则弹出其右与其左的两个操作数进行运算,然后将结果压入栈中,如图18所示。
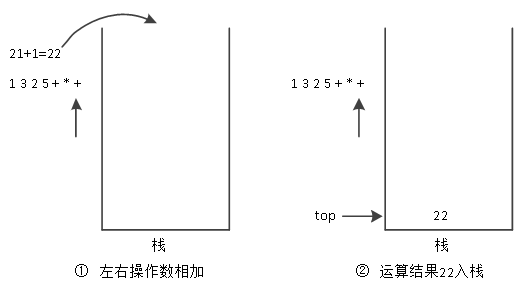
图18 运算结果22入栈
(6)继续读取,发现字符串遍历结束,且此时栈中只有一个元素,那么这个元素就是表达式的值。
经过上述分析得出的结果与我们用中缀表达式计算出的结果是一致的,证明计算机的这种“思维方式”是正确的。与中缀转后缀时的程序相同,这里同样可以使用3.2.2节中已经实现好的栈,即在Visual Studio2013中创建一个项目,将头文件linkstack.h与函数实现文件linkstack.c添加进来,只在main.c测试文件中编写程序。如例2所示。
例2
main.c //测试文件
1 #include "linkstack.h" //将栈的头文件包含进来
2 #include <stdio.h>
3
4 //判断字符是否是数字
5 int isNumber(char ch)
6 {
7 return (ch >= '0' && ch <= '9'); //是数字返回1,否则返回0
8 }
9
10 //判断字符是否是运算符
11 int isOperator(char ch)
12 {
13 return (ch == '+' || ch == '-' || ch == '*' || ch == '/');
14 }
15
16 //左右两个操作运算
17 int express(int left, int right, char op)
18 {
19 switch (op)
20 {
21 case '+':
22 return left + right;
23 case '-':
24 return left - right;
25 case '*':
26 return left * right;
27 case '/':
28 return left / right;
29 default:
30 break;
31 }
32 return -1;
33 }
34
35 //后缀表达式运算
36 int Calculate(const char * str)
37 {
38 LinkStack lstack = NULL;
39 lstack = Create();
40
41 int i = 0;
42 while (str[i]) //遍历字符串
43 {
44 if (isNumber(str[i])) //如果是数字,直接入栈
45 Push(lstack, str[i] - '0'); //在存储时按字符的ASCII码存储,所以送‘0’
46 else if (isOperator(str[i])) //如果是运算符,就弹出左右操作数
47 {
48 int left = Pop(lstack)->data;
49 int right = Pop(lstack)->data;
50 int ret = express(left, right, str[i]); //运算
51 Push(lstack, ret); //运算结果入栈
52 }
53 else
54 {
55 printf("error!\n");
56 break;
57 }
58 i++;
59 }
60
61 if (str[i] == '\0' && getSize(lstack) == 1)
62 return *((char*)getTop(lstack));
63 }
64
65 int main()
66 {
67 char *str = "1325+*+"; //正确的后缀表达式
68 int num = Calculate(str);
69 printf("%d\n", num);
70
71 system("pause");
72 return 0;
73 }运行结果如图19所示。

图19 例2运行结果
由图19可知,后缀表达式“1325+*+”的运行结果为22,是正确的。在例3-4中,代码36-63行是计算表达式结果的函数,它首先去遍历字符串,然后判断读取到的字符是数字还是运算符,如果是数字,则直接入栈,需要注意的是,因为字符在存储时是以其ASCII码值来存储的,例如将遍历到的字符“1”压入栈时,其实在栈中存储的值是其ASCII码值49,用这个值来参与计算显然是错误的,因此若要消去相应的差值,便需减去字符“0”的ASCII码值。
例2和例1一样,也是只能识别一位数的数据,当数据位数较多时就会出错,而且当运算式中有[]或{}符号时并无法识别。理论上说,一个好的程序不仅能运行出正确的结果,也要有一定的容错性,但由于篇幅的限制,本书就不再作相应实现。
