二叉树的顺序存储

二叉树的顺序存储也是用一组连续的存储单元来存放二叉树中的结点元素。对于完全二叉树来说，分配一段相应大小的空间，对树中的结点自上而下，自左至右进行存储，如图1所示，用数组对一棵完全二叉树进行存储。

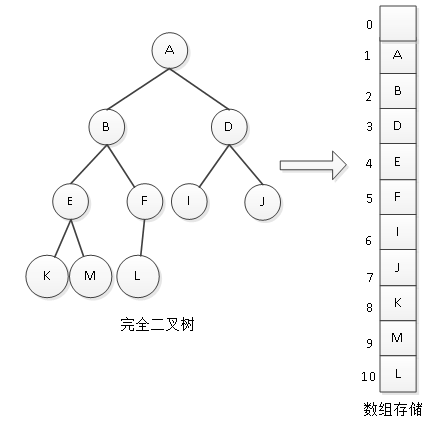
图1 完全二叉树的顺序存储

在顺序存储时， 0角标位置基本不用，从角标1开始存储。这样既存储了树中的结点元素，又存储了结点之间的逻辑关系。根据二叉树的性质5，知道了某一个结点元素的角标，那么它的父结点与孩子结点就能轻易找到。例如，对于结点元素D，其角标为3，那么它的父结点角标为⌊3/2⌋=1；如果它有孩子结点，其左孩子结点角标为2×3 = 6，右孩子结点角标为2×3+1=7。

在数组中查找角标1、6和7对应的结点元素：1角标为A，6角标为I，7角标为J；则D的双亲是A，左孩子是I，右孩子是J。这与左边完全二叉树的逻辑关系相同，因此根据完全二叉树的这个性质，我们可以将顺序存储中的完全二叉树还原出来。

对于完全二叉树，顺序存储与还原都没有问题，但对于一般的二叉树，如果仍按从上到下、从左到右的顺序将树中的结点顺序存储在一维数组中，数组元素下标之间的关系并不能反应出二叉树中结点之间的逻辑关系，如图2所示。

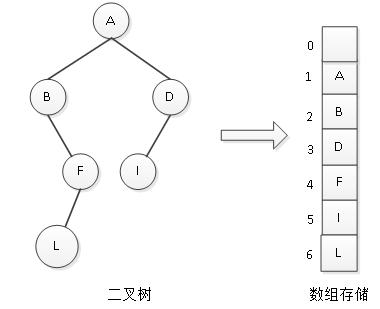
图2 一般二叉树的顺序存储

顺序存储图2中的一棵普通二叉树，则根据性质5并不能推断出结点之间的逻辑关系。

例如，同样对于3角标位上的元素D，其父结点角标应为⌊3/2⌋=1，1角标元素为A，在二叉树中是D结点的双亲，此逻辑关系正确；如果D结点有孩子，则其左孩子角标就为2×3=6，右孩子结点角标为2×3+1=7。在一维数组中，没有角标7，说明D不存在右孩子；而角标6为L，说明其左孩子为L，但在二叉树中，D结点的左孩子为I，因此此逻辑关系是错误的。

所以对于一般二叉树，并不能靠顺序存储来还原出一棵正确的二叉树。为了解决这个问题，可以在二叉树空缺的部分补上空结点，使之成为一棵完全二叉树，然后再用一维数组进行存储。如图3所示，将图2中的二叉树补全为一棵完全二叉树，然后再进行存储。

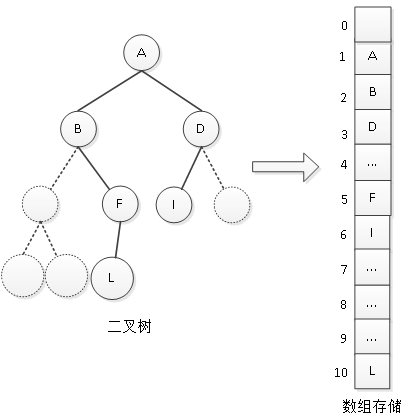
图3 补全二叉树的顺序存储

将二叉树用空结点补全为完全二叉树后，再进行顺序存储，同样以3角标位置的D元素为例，其父结点角标为3×2=1（取整数）；如果它有孩子结点，则左孩子结点角标为2×3=6，右孩子结点角标为2×3+1=7。通过一维数组中查找，1角标元素为A，即A为D的父结点；6角标元素为I，即I是D的左孩子；7角标为空，说明D没有右孩子。这与左边的二叉树的逻辑关系相同，这样就可以将二叉树正确地还原了。

对于完全二叉树而言，顺序存储既简单又节省内存空间，实用又方便。但对于一般二叉树，这样存储二叉树势必造成大量空间的浪费，最坏的情况下是右斜树，一棵深度为k的右斜树，只有k个结点，却需要分配2k-1个存储单元。当k很大时，这样的浪费是非常巨大的，因此一般二叉树不宜使用顺序存储。

顺序存储的二叉树在进行插入和删除操作时需要移动大量的结点，很不方便，因此在实际应用中顺序存储应用较少，但这种存储理念，读者应有所了解。