二叉树的遍历
1、先序遍历
先序遍历是指在遍历二叉树时先访问根结点,然后访问左子树,最后访问右子树。例如图6-26中的二叉树,使用先序遍历访问的结果是:ABFLDI。接下来我们就来详细分析这棵二叉树的先序遍历过程。
第一步:访问根结点,输出A;
第二步:访问左子树;左子树是以B为根结点的二叉树,如图1所示。
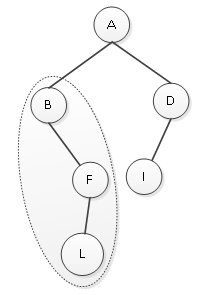
图1 以B为根结点的左子树
先遍历这棵左子树的根结点,输出B;
第三步:访问B的左子树,发现没有左子树,则访问B的右子树,右子树是以F为根结点的二叉树,先遍历这棵树的根结点,则输出F;
第四步:访问F的左子树,左子树是以L为根结点的二叉树,遍历这棵树的根结点,输出L;
第五步:访问L的左子树, L没有左子树;则访问L的右子树,L没有右子树;以L为根结点的二叉树访问完毕,即F的左子树访问完毕;
第六步:访问F的右子树,发现F没有右子树,则以F为根结点的二叉树访问完毕,即B的右子树访问完毕,那么以B为根结点的二叉树就访问完毕,即A的左子树访问完毕;
第七步:访问A的右子树,右子树是以D为根结点的二叉树,先遍历根结点,则输出D;
第八步:遍历D的左子树,左子树是以I为根结点的二叉树,先遍历根结点,则输出I;
第九步:访问I的左子树,左子树不存在;访问I的右子树,右子树不存在;则以I为根结点的二叉树访问完毕,即D的左子树遍历完毕;
第十步:访问D的右子树,D没有右子树;则以D为根结点的二叉树访问完毕,即A的右子树遍历完毕,整棵树也遍历完毕;
这就是二叉树的先序遍历的过程,按上述分析步骤输出的结果为:ABFLDI。树是递归定义的,在遍历二叉树时也用到了递归,首先将整棵二叉树当作有三个单元的结构:根结点、左子树、右子树。遍历完根结点,开始遍历左子树时,把左子树当成一棵独立的二叉树来遍历;同样,当遍历右子树时,也将右子树当成一棵独立的二叉树来遍历,这就是递归的思想。
有了递归的思想,在实现先序遍历算法时就容易多了。很容易想到函数递归调用:将代表一棵树的根结点传入函数,遍历完根结点后,再将左子树作为一棵完整的二叉树传递给函数,等左子树遍历完成后,再将右子树作为一棵完整的二叉树传递给函数。代码如下所示:
void preOrder(BitNode* T)
{
//遍历根节点
if (T == NULL)
return;
printf("%c", T->data); //输出根结点的值
//遍历左子树
if (T->lchild != NULL)
preOrder(T->lchild); //递归调用
//遍历右子树
if (T->rchild != NULL)
preOrder(T->rchild); //递归调用
}2、中序遍历
有了先序遍历的经验,那么中序与后序遍历就好理解了,中序遍历就是先访问树的左子树,然后访问根结点,最后访问右子树,如果使用中序遍历输出图1中的二叉树,则结果为:BLFAID。
下面来分析中序遍历的过程:
第一步:先访问根结点A的左子树;左子树是以B为根结点的二叉树,再访问B的左子树,B没有左子树;则访问根结点B,输出B;
第二步:访问B的右子树,右子树是以F为根结点的二叉树;
第三步:访问F的左子树,F的左子树是以L为根结点的二叉树;
第四步:访问L的左子树,左子树不存在,访问根结点L并输出;
第五步:访问L的右子树,右子树不存在;则以L为根结点的二叉树访问完毕,即F的左子树访问完毕;访问根结点F并输出;
第六步:访问F的右子树,右子树不存在。则F的右子树访问完毕,以F为根结点的二叉树访问完毕,即B的右子树访问完毕,以B为根结点的二叉树访问完毕,即A的左子树访问完毕;
第七步:访问根结点A并输出;
第八步:访问A的右子树,A的右子树是以D为根结点的二叉树;
第九步:访问D的左子树,D的左子树是以I为根结点的二叉树;
第十步:访问I的左子树,左子树不存在;访问根结点I并输出;
第十一步:访问I的右子树,右子树不存在;则以I为根结点的二叉树访问完毕,即D的左子树访问完毕;访问根结点D并输出;
第十二步:访问D的右子树,右子树不存在;则以D为根结点的二叉树访问完毕,即A的右子树访问完毕;整棵树访问完毕;
分析得出的遍历结果为:BLFAID。中序遍历的代码实现如下所示:
void inOrder(BitNode* T)
{
if (T == NULL)
return;
//遍历左子树
if (T->lchild != NULL)
inOrder(T->lchild); //递归调用
//遍历根结点
printf("%c", T->data);
//遍历右子树
if (T->rchild != NULL)
inOrder(T->rchild);
}3、后序遍历
后序遍历就是先访问树的左子树,然后访问树的右子树,最后访问根结点。图6-26中的二叉树按后序遍历输出,则输出结果为:LFBIDA。
前面已经详细分析了树的先序遍历与中序遍历,这里就不再给出后序遍历的详细过程,读者可根据先序和中序的遍历过程思想来分析后序遍历。后序遍历同样也是利用了递归的思想,大树之中套小树。
后序遍历算法的代码实现如下所示:
void lastOrder(BitNode* T)
{
if (T == NULL)
return;
//遍历左子树
if (T->lchild != NULL)
lastOrder(T->lchild); //递归调用
//遍历右子树
if (T->rchild != NULL)
lastOrder(T->rchild);
//遍历根结点
printf("%c", T->data);
}接下来构建图6-26中的二叉树,并分别用先序、中序和后序遍历来输出这棵二叉树。三种遍历算法在讲解时已经给出,在案例中直接调用即可。具体代码如例1所示。
例1
1 #include <stdio.h>
2 #include <stdlib.h>
3 typedef struct BitNode
4 {
5 char data; //数据类型为char
6 struct BitNode* lchild, *rchild;
7 }BitNode;
8
9 int main()
10 {
11 BitNode nodeA, nodeB, nodeD, nodeF, nodeI, nodeL; //创建6个结点
12 //将结点都初始化为空,保证叶子结点相应指针指向空
13 memset(&nodeA, 0, sizeof(BitNode));
14 memset(&nodeB, 0, sizeof(BitNode));
15 memset(&nodeD, 0, sizeof(BitNode));
16 memset(&nodeF, 0, sizeof(BitNode));
17 memset(&nodeI, 0, sizeof(BitNode));
18 memset(&nodeL, 0, sizeof(BitNode));
19 //给结点赋值
20 nodeA.data = 'A';
21 nodeB.data = 'B';
22 nodeD.data = 'D';
23 nodeF.data = 'F';
24 nodeI.data = 'I';
25 nodeL.data = 'L';
26 //存储结点之间的逻辑关系
27 nodeA.lchild = &nodeB; //A结点左孩子是B
28 nodeA.rchild = &nodeD; //A结点的右孩子是D
29 nodeB.rchild = &nodeF; //B结点的右孩子是F
30 nodeF.lchild = &nodeL; //F结点的左孩子是L
31 nodeD.lchild = &nodeI; //D结点的左孩子是I
32
33 printf("二叉树构建成功!\n");
34
35 printf("先序遍历:");
36 preOrder(&nodeA);
37
38 printf("\n中序遍历:");
39 inOrder(&nodeA);
40
41 printf("\n后序遍历:");
42 lastOrder(&nodeA);
43 printf("\n");
44 system("pause");
45 return 0;
46 }运行结果如图2所示。
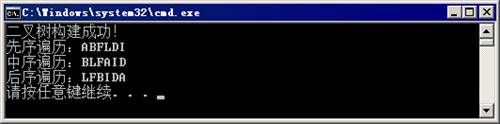
图2 例1运行结果
在例1中,首先构建了图1中的二叉树,然后分别用先序、中序及后序遍历来访问这棵树,对比可知,图2中先序、中序及后序遍历的输出结果与前文分析的一致。
二叉树遍历算法分析:从前面的三种遍历算法可知道,如果将printf()语句抹去,从递归的角度看,这三种算法完全相同,或都说这三种算法访问的路径是相同的,只是访问结点的时机不同而已。针对图1中构建的二叉树,以结点B为例,遍历结点时,它有3次被访问的时机,如图3所示。
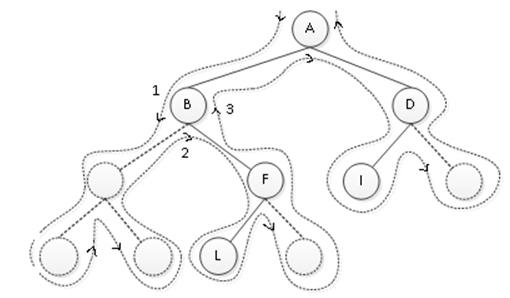
图3 二叉结的遍历路径
从A结点出发,到回到A结点的遍历路径中,如图中所标识1、2、3所示,一共经过结点B 3次。其实从虚线的出发点到终点,每个结点都有3次被访问的机会:
第一次经过时访问就是先序遍历;
第二次经过时访问就是中序遍历;
第三次经过时访问就是后序遍历;
访问路径相同,只是访问结点的时机不同,这是二叉树遍历的本质。
二叉树的遍历,从时间上来说,每个结点只被访问一次,其时间效率是O(n);从空间上来说,要按照树占用的最大辅助空间来算,例如,图3中,这是一棵补全的完全二叉树,那么在计算时,要把这些辅助空间也计算在内,因此其空间效率也是O(n)。
