递归思想的应用
二叉树的遍历是非常重要的,特别是遍历中递归思想的应用,递归在树的学习中非常重要,它几乎在树的所有操作中都有体现,为了加强读者对树的递归思想的理解、掌握与应用,本节来讲解几个关于树中递归思想应用的算法。
1、求二叉树的叶子结点的个数
求二叉树的叶子结点个数比较简单,用任何一种遍历算法遍历二叉树,凡是树中结点左右指针都为空者就是叶子结点,将其统计并打印出来。其算法思想如下:
(1) 二叉树的叶子结点个数是左子树叶子结点和右子树叶子结点个数之和。
(2) 左子树又可视为一棵独立的二叉树,它的叶子结点个数是其左子树和右子树叶子结点数之和;
(3) 右子树也可视为一棵独立的二叉树,它的叶子结点个数是其左子树和右子树叶子结点数之和;
……
这样不断地递归,直到二叉树遍历完毕,就可算出叶子结点的个数。其对应算法实现如下所示:
//求叶子结点个数
int sum = 0; //记录叶子节点个数
void getLeafNum(BitNode* T)
{
if (T == NULL)
return;
if (T->lchild == NULL && T->rchild == NULL) //左右孩子指针均为空,就是叶子结点
sum++; //叶子结点个数加1
getLeafNum(T->lchild); //递归调用函数求算左子树叶子结点个数
getLeafNum(T->rchild); //递归调用函数求算右子树叶子结点个数
}函数getLeafNum()中递归调用自身来求算左右子树的叶子结点个数,上节案例中构建了一棵二叉树,读者可调用此算法求出二叉树的叶子节点个数。
2、求二叉树的高度
在一棵二叉树中,根结点是树中的第一层,求其左子树与右子树的高度,比较左右子树的高度,取较大的值加上根结点的高度1就是整棵树的高度。如图1所示。
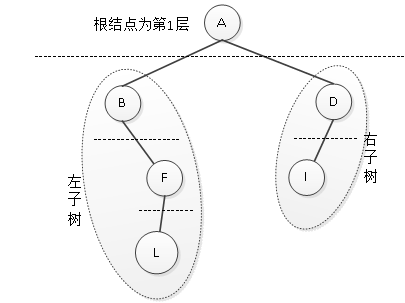
图1 求树的高度
图1中的二叉树,左子树高度为3,右子树高度为2,则取左子树的高度与根结点的一层高度相加,3+1=4,得知此树的高度为4。
在求左子树与右子树的高度时,将左右子树分别视为一棵独立的二叉树,根节点是树的第一层高度,分别求左右子树的高度。这明显也是递归思想的应用,其代码实现如下所示:
//求树的高度
int Depth(BitNode* T)
{
int depth = 0;
int dleft = 0, dright = 0; //分别定义左右子树高度
if(T == NULL)
return 0;
dleft = Depth(T->lchild); //求左子树的高度
dright = Depth(T->rchild); //求右子树的高度
//去左右子树高度中较大的一个1相加并返回
return 1 + (dleft > dright ? dleft : dright);
}此算法也是函数的递归调用,读者可在例6-2中调用此算法来求出树的高度。
3、拷贝二叉树
拷贝二叉树需要逐个的拷贝树中结点,不管树有多么复杂, 都可以分为三个部分:根结点、左子树、右子树。
在拷贝时,可以分三个步骤来完成拷贝:
(1)为新树分配新的根结点;
(2)先拷贝左子树,再拷贝右子树;新根结点的左孩子指针指向拷贝过来的左子树,右孩子指针指向拷贝过来的右子树;
(3)如果左右子树是一棵树,重复步骤(1)、(2)、(3);
此算法代码实现如下所示:
//拷贝二叉树
BitNode* copyTree(BitNode* T)
{
//分配节点与指向左右子树的指针
BitNode* newT = (BitNode*)malloc(sizeof(BitNode)); //新树根节点
BitNode* newlchild = NULL; //新树的左子树指针
BitNode* newrchild = NULL; //新树的右子树指针
if (newT == NULL)
return NULL;
if (T == NULL)
return NULL;
newlchild = copyTree(T->lchild); //拷贝左子树
newrchild = copyTree(T->rchild); //拷贝右子树
//新树根结点的左孩子指针指向左子树,右孩子指针指向右子树
newT->data = T->data;
newT->lchild = newlchild;
newT->rchild = newrchild;
return newT;
}读者可以在上节案例中调用此算法拷贝出一棵新的二叉树,然后调用任一种遍历算法进行输出,判断新的二叉树是否和原来的二叉树一样。
这三个算法都是递归在二叉树应用中的体现,读者要好好理解掌握。
