二叉树与树之间的转换

树转换为二叉树，其实在前面章节中已经讲解过，树的表示法中，第3种左孩子右兄弟表示其实就是讲解如何将一棵树转换为二叉树，转化的原则是由“兄长”照管“幼弟”，右边的孩子交由左边的孩子照管，左边的孩子交由其更左边的孩子照管，到最后，只保留父结点与最左边长子的连线。

关于树转换为二叉树，前面章节中已有详细讲解，这里就不再赘述，只是要注意一点：由于树根没有兄弟，帮树转化为二叉树后，二叉树根结点的右子树必为空。

树可以转换为二叉树，自然二叉树也可以还原为原来的树。并非任意一棵二叉树都能还原成一般树，此时的二叉树必须是由某一棵树（一般树）转换而来的、根结点没有右子树的二叉树。将二叉树转换为树是树转换为二叉树的逆过程，其步骤如下：

（1）加线：若某个结点i是其父结点的左孩子，则将结点i的右孩子，右孩子的右孩子……全部与i的父结点用虚线连接，当且仅当连续地沿着右孩子的右链不断搜索到的所有右孩子，都分别与结点i的父结点用虚线连接。

（2）去线：把原二叉树中所有父结点与其右孩子的连线抹去。这些右孩子实质上是其父结点的兄弟。

（3）整理：把虚线改为实线，调整层次结构。

按照上述步骤，以“树的表示法”一节图7中的二叉树为例，演示还原的过程。

第一步：加线（虚线），将树中每条右链中的所以右孩子都连接到右链链头结点的父结点上，如图1所示。

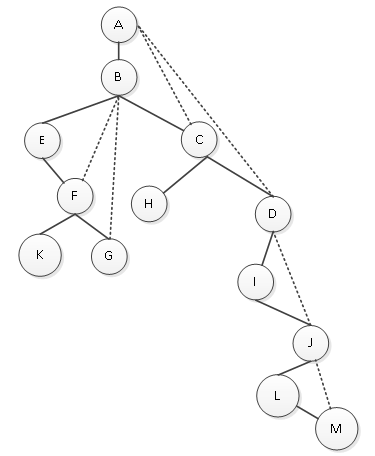
图1 加线

第二步是去线，将原二叉树中父结点与其右孩子的连线抹去，如图2所示。

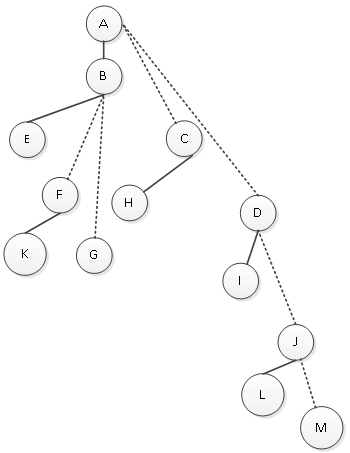
图2 去线

第三步整理，去掉原二叉树中的连接线后，将新的连接线由虚线变为实线，调整树中结点的层次结构，调整的结果如图3所示。

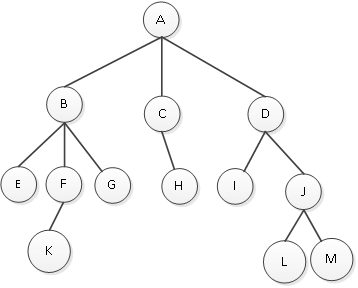
图4 还原的树

图4中就是被还原的树，在这里有一个问题读者须留意，结点C只有一个孩子H，在还原后，H是放在左边还是右边，这个并不影响树的结构，因为树是无序的。