中序和先序构建二叉树

在学习之前，先来看一道题：现有一棵二叉树，已知该树中序遍历的结果为“ABCDE”，请问它是否能唯一确定一棵二叉树？

经过思考之后，答案显然是否定的，只根据中序遍历得到的结果，很容易就能构建出多种二叉树的结构，如图1所示。

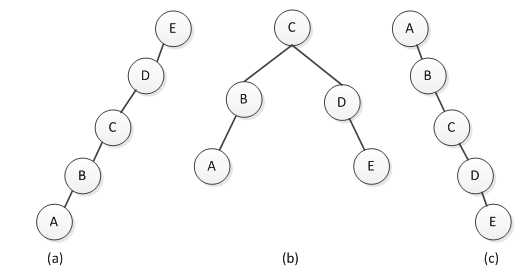
图1 根据中序遍历结果“ABCDE”构造的二叉树

除了图1中的三棵二叉树，还可以构造出其他结构的二叉树。由这个例子可以明确得出：只通过这一种顺序的遍历结果无法唯一确定一棵树的结构。同样的，通过先序或后序遍历的结果也无法唯一确定一棵二叉树的结构。

那么如何才能确定一棵树的结构呢？想要通过遍历结果来确定一棵树需要将两种顺序的遍历结果结合起来。结合方案有以下两种：

● 中序遍历结果和先序遍历结果一起可以确定一棵二叉树；

● 中序遍历结果和后序遍历结果一起可以确定一棵二叉树。

注意：即便结合先序遍历和后序遍历的结果也无法确定一棵二叉树的的结构，因为这两种遍历结果结合只能求解出根，不能确定左子树什么时候结束，右子树什么时候开始。

根据中序遍历和先序遍历结果确定二叉树结构的基本思路如下：

（1）通过先序遍历找到根结点，再通过根节点在中序遍历的位置找出左子树、右子树；

（2）根据左子树在先序遍历结果的顺序，找到左子树的根结点，视左子树为一棵独立的树，转步骤（1）；

（3）根据右子树在先序遍历结果的顺序，找到右子树的根结点，视右子树为一棵独立的树，转步骤（1）。

假如有一棵二叉树，它的先序遍历结果为：ADEBCF；中序遍历结果为：DEACFB。则确定此二叉树的步骤如下：

第一步：由先序遍历结果可知，此二叉树的根结点为A；再结合中序遍历结果，可知A的左子树为DE，右子树为CFB，如图2所示。

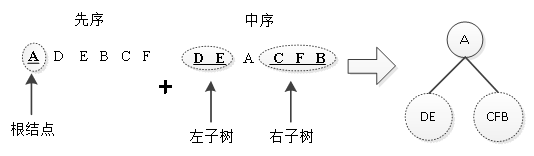
图2 根结点A与其左右子树

第二步：A的左子树中包含有DE两个结点，由先序遍历结果可知，D结点在E的前面，那么D是左子树的根结点；又因在中序遍历中，E结点在根结点D之后，先遍历D后遍历E，说明D是根结点，E是D的右孩子。由此A的左子树可以确定，如图3所示。

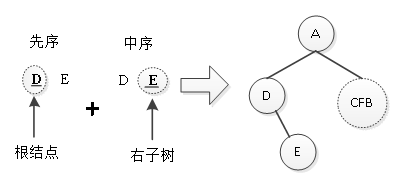
图3 确定A的左子树

第三步：由整棵树的先序遍历结果可知右子树的先序遍历结果为：CFB，因此B是右子树的根结点；又因为在中序遍历中，CF都在B之前，说明C、F是B的左子树结点；

对以B为根节点的子树继续分析：在先序遍历中，C在F的前面，说明在B的左子树中，C是根结点；在中序遍历中：F在C的后面，说明F是C的右孩子；由此，A的右子树也确定下来，这个过程如图4所示。

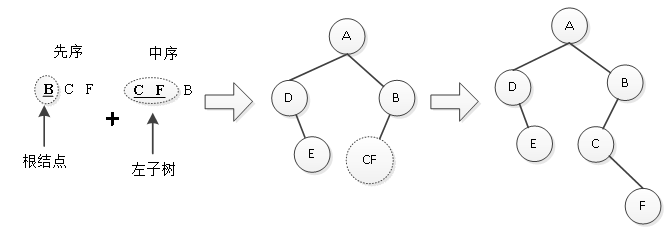
图4 确定A的右子树

这三个步骤分别确定了二叉树的根结点、左子树与右子树，这样就确定了一棵二叉树。其实这个求算过程也是递归的，当根结点的左子树或右子树是一棵独立的二叉树时，便需递归调用（1）（2） （3）来确定子树。

相比于遍历来说，二叉树的创建稍有难度，读者应在理解的基础上加以练习，以期熟练掌握本小节学习内容。