#号法创建树
由上一节的学习我们知道,单独使用先序遍历结果无法唯一确定一棵二叉树,但如果用#号法,先序遍历结果就可以唯一确定一棵二叉树。
什么是#号法呢?#号法就是让树的每一个结点都变成度数为2的树,度不为2的结点就用“#”符号补齐,如图1所示,就是一棵#号法创建的二叉树。

图1 结点度数都为2的二叉树
这样,所有的结点度数都为2,先序遍历这棵二叉树的结果为:AD#E##BC#F###。“#”号法创建二叉树有一个特点:叶子结点后面至少有两个“#”号。
假设有一棵二叉树先序遍历结果为:DFE###B##。下面我们就来分析如何使用这个结果如何唯一确定一棵二叉树。
第一步:先序遍历,那么D就是这棵树的根结点;D的左孩子为F,F的左孩子为E,如图2所示。

图2 确定D、F、E三个结点
第二步:E结点后面紧跟了两个“#”符号,则E为叶子结点,如图3所示。
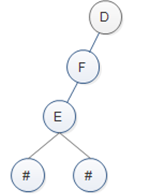
图3 E为叶子结点
第三步:E后面还有第三个“#”符号,则这个符号必为F的右孩子,如图4所示。
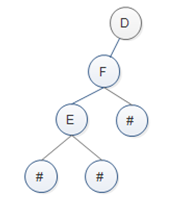
图4 F的右孩子确定
至此,D的左子树构造完毕。
第四步:D的右子树为B##,B为一个叶子结点。则整棵树如图5所示。
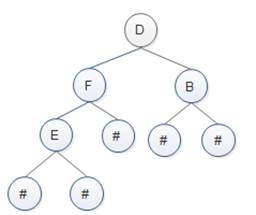
图5 完整的二叉树
这就是由#号法来创建树,也比较易于理解。但是须注意:#号法只能用于先序遍历,因为在中序和后序遍历中无法确定树的根结点,因此不能唯一确定一棵树。
理解了#号法构建树的原理,那么算法实现起来也就很容易理解了,接下来我们通过一案例来用#号法构建一棵树,然后用中序遍历将这棵输出,最后将这棵树释放。具体如例1所示。
例1
1 #define _CRT_SECURE_NO_WARNINGS
2 #include <stdio.h>
3 #include <stdlib.h>
4
5 typedef struct BitNode
6 {
7 char data;
8 struct BitNode* lchild, *rchild;
9 }BitNode;
10
11 //中序遍历
12 void inOrder(BitNode* T)
13 {
14 if (T == NULL)
15 return;
16 //遍历左子树
17 if (T->lchild != NULL)
18 inOrder(T->lchild); //递归调用
19
20 printf("%c", T->data); //遍历根节点
21
22 //遍历右子树
23 if (T->rchild != NULL)
24 inOrder(T->rchild);
25 }
26
27 //#号法创建二叉树
28 BitNode* BitNode_Create()
29 {
30 BitNode* temp = NULL;
31 char ch;
32 scanf("%c", &ch);
33 if (ch == '#') //如果输入#号,则返回NULL
34 {
35 temp = NULL;
36 return temp;
37 }
38 else
39 {
40 temp = (BitNode*)malloc(sizeof(BitNode)); //为结点分配空间
41 if (temp == NULL)
42 return NULL;
43 temp->data = ch;
44 temp->lchild = NULL;
45 temp->rchild = NULL;
46 //创建结点的左右子树
47 temp->lchild = BitNode_Create();
48 temp->rchild = BitNode_Create();
49 return temp;
50 }
51 }
52
53 //释放树:先释放左子树,再释放右子树,最后释放根结点
54 void BitNode_Free(BitNode* T)
55 {
56 if (T == NULL)
57 return;
58 if (T->lchild != NULL)
59 {
60 BitNode_Free(T->lchild); //释放左子树
61 T->lchild = NULL;
62 }
63 if (T->rchild != NULL)
64 {
65 BitNode_Free(T->rchild); //释放右子树
66 T->rchild = NULL;
67 }
68 free(T);
69 }
70
71 int main()
72 {
73 BitNode* T = NULL;
74 printf("请输入树的结点元素值:\n");
75 T = BitNode_Create(); //创建树
76
77 inOrder(T); //中序遍历此树
78 printf("\n");
79 BitNode_Free(T);
80 printf("二叉树释放成功!\n");
81
82 system("pause");
83 return 0;
84 }运行结果如图6所示。
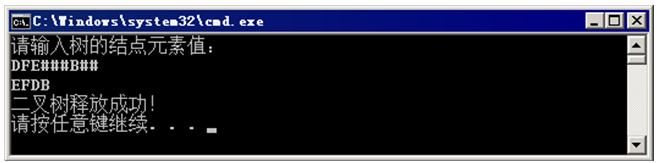
图6 例1运行结果
在例1中,代码28-51中用#号法来构建二叉树,创建根结点,并从键盘输入结点元素值:如果输入的是“#”符号,则根结点为NULL;如果输入的是字符,则为根结点分配空间,并赋值,且使左右子树为NULL。然后递归调用函数分别构建左右子树;
代码54-69行中释放树,在释放树时先释放树的左子树再释放树的右子树,最后释放根结点。注意:不能先释放根结点,否则找不到左右子树,便无法对左右子树进行释放。
在运行时输入了“DFE###B##”字符串,构建出了图6-57中的二叉树,然后中序遍历此树,由图6可知结果为“EFDB”。
