关键路径

拓扑排序将活动抽象为顶点，研究一个工程中多个活动之间的次序问题。但是有时候，除了关注多个活动的先后顺序，我们还关心完成整个工程所花费的时间。

1、AOE-网和关键路径

假设现有一工程，我们将其中的活动抽象为边，边上的权值表示该活动持续的时间；将其中的事件抽象为顶点，表示在此之前的活动已经完成，在此之后的活动可以开始。这样一个工程可以抽象为一个网图，我们称其为AOE-网（activity on edge），即用边表示的网。它对应AOV-网，常用于表示工程流程。工程中的活动往往是有次序的，所以以下分析基于AOE-网已经拓扑有序。

以图1中的AOE网图为例。

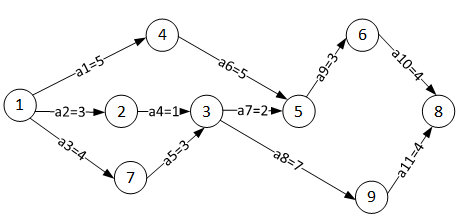
图1 AOE-网示例

图1中的AOE-网有9个事件v1~v9，11个活动a1~a11。举例学习AOE网中事件和活动的定义：事件v1表示整个工程的开始，此时可以开始执行活动a1、a2、a3；事件v5表示活动a6和活动a7已完成，活动a9可以开始；事件v8表示整个工程的结束。假设边上的权值以天为单位，其中活动a1持续的时间为5天，活动a2持续的时间为3天，以此类推。

一个AOE-网中只有一个入度为零的顶点和一个出度为零的顶点，分别用于指代一个工程中的开始点和完成点，通常称入度为零的顶点为源点，称出度为零的顶点为汇点。

从图中一个顶点到达另外一个顶点的路径可能不止一条，每条路径上的活动依次执行，不同路径上的活动可以并行执行。路径可以视为工程中的流水线。依照图1，v1为源点，v8为汇点。在事件v3触发时，活动a4和活动a5已完成，活动a7和活动a8可以开始。从源点v1开始，到触发事件v3，需要完成的活动为a2、a4，与活动a3、a5。完成路径v1->v2->v3上的活动所需时间为3+1=4天；完成路径v1->v7->v3上的活动所需时间为4+3=7天。

AOE-网图既是用来表示工程流程的，那么图中的所有事件都必须触发，该工程才算完成。对于活动ak，只有它的弧头事件v触发了，它才可以开始执行；而对于事件v，只有所有以它为弧尾的活动全部完成，它才会被触发。那么，从一个事件触发到另一个事件触发的工期，应该是其间每条路径上多个活动工期之和中的最大值。例如从事件v1开始，到事件v3触发，所花费的时间应为7天。

依此类推，触发事件v5时花费的时间为10天，触发事件v8时花费的时间为18天。

我们把路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径称为关键路径，在关键路径上的活动称为关键活动。显然在前面小节中，路径v1->v7->v3->v9->v8即为关键路径，路径长度为18，事件a8触发，代表着整个工程全部完成，所以整个工程的工期为18天。

若考虑加快一个工程的进度，应该缩短其关键活动花费的时间。以图1中的AOE-网图为例，即使活动a2的时间缩短为1，对整个工程周期也毫无影响，因为通过路径v1->v2->v3到达v3之后，还要等待路径v1->v7->v3中的活动全部完成，否则无法触发事件v3。因此， 应该通过缩短活动a3、a5、a8、a11的执行时间以达到缩短工期的目的。当然，在缩短关键活动持续时间时，可能会获得新的关键路径，这时应该尽量缩短新路径中关键活动花费的时间。

2、关键路径求解分析

从关键路径的学习中了解到，触发一个事件需要完成该事件之前的所有活动。从事件vi到事件vj，之间的路径可能不止一条，这些路径中关键路径上的活动需要花费的时间最久。假设关键路径上的活动执行的时间为ti~tj，其中ti为活动事件vi触发的时刻，tj为事件vj触发的时刻。那么只要保证非关键路径上的活动，在时间ti~tj之间完成即可。

从源点v1到顶点vi最长路径长度（即关键路径的长度）的数值，为顶点（事件）vi的最早发生时间，记为ve。根据分析，网中任一事件v的最早发生时间为

ve(v)=MAX {c(p)}

其中c(p)表示路径p的长度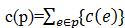， ，{c(p)}为所有路径长度的集合。以图1中的AOE-网为例，事件v3的最早发生时间，是关键路径v1->v7->v3的长度7，此时以v3为弧头的活动a7、a8可以开始执行。AOE-网的工期为汇点v的最早发生时间，前面图中AOE-网的工期T为汇点v8的最早发生时间，即T=ve(8)=18。

对应最早发生时间，给出最晚发生时间的定义，即：在不推迟整个工程进度的前提下，事件v最晚必须发生的时间，记为vl(v)。假设事件vi到事件vj之间有路径，那么

vl(i)=ve(j)- MAX{c(p)}

对于AOE-网，假设给定的工期是20，已知它实际需要工期为18，那么此时vl(i)=vl(1)，ve(j)=ve(8)=20，MAX{c(p)}=18，其源点v1的最晚发生时间为2。

每个活动ak=<v,w>有个最早开始时间，即活动最早可以开始执行的时间。用e(k)表示活动ak的最早开始时间，这个时间由事件vi的最早发生时间决定。假设顶点v为活动ak所在边的弧头，那么

e(k)=ve(v)

对于前面小节图中AOE-网，ve(3)=7，所以事件v3后活动a7和活动a8的最早开始时间为7，记为e(7)=7，e(8)=7。

对应最早开始时间，用l(k)表示活动ak的最晚开始时间。l(k)指在不推迟工期的前提下，活动ak最晚必须开始的时间。这个时间等于该活动弧头的最晚发生时间，假设顶点v为活动ak所在边的弧头，那么

l(k)= vl(v)

假设关键路径上的活动安排紧凑，当前活动执行完毕，立刻开始执行其后的活动。那么关键路径上关键活动花费的时间总和，即为该工程的工期。非关键路径上的活动ak有一定的空闲时间，其值为l(k)-e(k)，活动ak可以在空闲时间允许的范围内推迟。

综上，非关键路径上的活动时间加上空闲时间等于关键路径的路径长度，关键路径的路径长度等于路径上所有关键活动的执行时间。

关键活动没有空闲时间，那么它的最早开始时间和最晚开始时间必然相同。求解关键路径中关键活动的核心思想是：比较活动的最早开始时间和最晚开始时间，如果时间相同，表示该活动是关键活动，活动之间的弧是关键路径的组成部分；否则反之。

求解关键路径，找到关键活动，对关键活动的执行时间进行控制，这也是求关键路径的意义。

在AOE-网中，假设活动ai和活动aj所在的边首尾相连，ai=<v,w>，aj=<w,y>，那么称活动aj是活动ai的后继，活动ai是活动aj的前驱。设源点到顶点v的路径长度为t1，顶点w到汇点的路径长度为t2，源点到汇点的路径长度为t，那么：

（1）事件v的最早发生时间，即活动ai的最早开始时间为e(i)=ve(v)=t1；

（2）事件w的最早发生时间，即活动aj的最早开始时间e(j)=ve(w)=ve(v)+MAX{c<v,w>}（v w）。

（3）事件w的最晚发生时间，即活动aj的最晚开始时间为l(j)=vl(w)=t-t2=vl(y)-aj；

（4）事件v的最晚发生时间，即活动ai的最晚开始时间为e(i)=ve(v)=vl(w)-MIN{c<v,w>}（v w）。

根据（1）（2）可知，求当前活动的最早开始时间，即求从源点到该活动弧头顶点的最长路径长度；求其后继活动的最早开始时间，必须知晓当前活动的最早开始时间和执行活动所需时间。所以求顶点最早开始时间是一个递推过程。设源点a的最早发生时间为0，那么最早发生时间求解公式为：

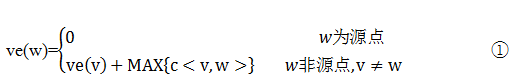
公式①中之所以是ve(v)+MAX ，而非ve(v)+c<v,w>，是因为在求解的过程中，顶点v和顶点w之间可能产生新的路径。如图2所示，顶点v1和顶点v2之间有直接路径a1，路径长度为5，此时MAX{c<v,w>}初始化为5；在逐步遍历的过程中（假设先遍历完顶点v3和顶点v4），得到新的路径v1->v3->v4->v2，路径长度为6， MAX{c<v,w>}替换为6；之后遍历了顶点v5，获得新的路径v1->v5->v2，路径长度为7， MAX{c<v,w>}被替换为7。要明白<v,w>之间的路径长度初始化为活动ak的执行时间，但是在后来遍历的过程中可能会发生改变。这里假设顶点v1~v5的顺序序列为一个拓扑序列。

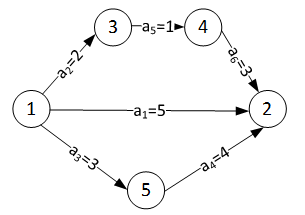
图2 v1到v2边与路径示例

根据（3）（4）可知，求当前活动的最晚开始时间，即求完整工期与当前活动弧头顶点到汇点长度的差值；求其前驱活动的最晚开始时间，必须知晓当前活动的最晚开始时间和执行当前活动所需花费的时间。所以求顶点最晚开始时间同样是一个递推过程。设汇点b的最晚发生时间为e(v)，那么最晚发生时间求解公式为：

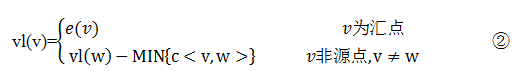
公式②中的MIN与公式①中的MAX同理。

综上分析，可知无论是最早开始时间还是最晚开始时间都由递推公式求得，所以需要按照既定的序列依次对每个顶点求解。对于最早开始时间求解，这个既定序列是AOE-网的一个拓扑序列；对于最晚开始时间求解，这个既定序列是AOE-网的一个逆拓扑序列。对于网中的每个活动，只要按照次序，反复运用递推公式，便可求出其最早开始时间和最晚开始时间。

3、关键路径算法与分析

因为求关键路径时需要求AOE-网的拓扑序列，所以使用7.6中给出的图的邻接表存储定义来存储图，同时在邻接表中保留了网图的权值。求关键路径的算法中要求解网的拓扑序列，并依次求解事件的最早发生时间，因此需要对7.6中的拓扑算法稍作修改，加入对事件最早发生时间的求解。

综合本小节对关键路径以及其求解方法的分析，总结出以下求AOE-网关键活动的主要步骤：

（1）对于源点a，设置ve(a)=0；

（2）对AOE-网进行拓扑排序，若发现回路，排序失败，退出程序；否则存储拓扑序列，继续执行；

（3）按照顶点a的拓扑次序，反复执行递推公式①，求除源点外其余顶点的ve(v)值；

（4）对其汇点b，设置vl(b)=ve(b)，也就是将汇点b的最早发生时间作为最晚发生时间，其实际意义是工程的实际工期等于预计工期，整个工程没有空闲时间；

（5）按照顶点a拓扑序列的逆序，反复执行递推公式②，求除汇点外其余顶点的vl(w)值；

（6）活动ak=<v,w>的最早开始时间e(k)是其弧头顶点表示事件的最早开始时间，e(k)=

ve(v)；

（7）活动ak=<v,w>的最晚开始时间l(k)是其弧尾顶点表示事件的最晚发生时间与执行该活动所需时间的差值，即l(k)=ve(w)-ak；

（8）关键活动没有空闲时间，即e(k)=l(k)，表示活动ak的最早开始时间e(k)等于其最晚开始时间l(k)，该活动是关键活动。

下面首先给出修改后的拓扑排序算法。该算法涵盖了主要步骤（1）（2）（3）。

//修改后的拓扑排序算法
int *ve, *vl;            //记录事件最早发生时间和最晚发生时间
int *stack2;            //用于存储拓扑序列的栈
int top2;                //用于stack2的指针
//拓扑排序
int TopologicalSort(GraphAdjList *G)
{
    ArcNode *e;
    int i, k, gettop;
    int top = 0;        //用于栈指针下标
    int count = 0;        //用于统计输出顶点的个数
    int *stack;            //创建栈将入度为0的顶点入栈
    stack = (int*)malloc(G->n*sizeof(int));
    for (i = 0; i < G->n; i++)
    {
        if (0 == G->adjList[i].indegree)
            stack[++top] = i;
    }
    top2 = 0;                                    //初始化为0
    ve = (int*)malloc(G->n*sizeof(int));        //事件最早发生时间
    for (i = 0; i < G->n; i++)
        ve[i] = 0;                                //(1)初始化为0
    stack2 = (int*)malloc(G->n*sizeof(int));    //初始化
    while (top != 0)
    {
        gettop = stack[top--];
        count++;
        stack2[++top2] = gettop;                //将弹出的顶点序号压入拓扑序列的栈
        for (e = G->adjList[gettop].firstarc; e; e = e->next)
        {
            k = e->adjvex;
            if (!(--G->adjList[k].indegree))
                stack[++top] = k;
              //(3)求各顶点事件最早发生时间
            if ((ve[gettop] + e->weight) > ve[k])    
                ve[k] = ve[gettop] + e->weight;
        }
    }
    if (count < G->n)
     {
         printf("\n该有向图有回路，无法完成拓扑排序！\n");
        return -1;
     }
    else
        return 0;
}

求解关键路径的算法如下。该算法涵盖步骤（4）（5）（6）（7）（8）。

//求关键路径
void CriticalPath(GraphAdjList *G)
{
    ArcNode *e;
    int i, gettop, k, j;
    int e, l;                //声明活动最早发生时间和最晚发生时间
    TopologicalSort(&G);    //(3)求拓扑序列，计算数组ve和stack2的值
    vl = (int*)malloc(G->n*sizeof(int));        //事件最晚发生时间
    for (i = 0; i < G->n; i++)
        vl[i] = ve[G->n - 1];                    //初始化vl
    while (top2 != 0)
    {
        gettop = stack2[top2--];                //将拓扑序列出栈
        for (e = G->adjList[gettop].firstarc; e; e = e->next)
        {
            k = e->adjvex;
               //(6)求各个顶点事件发生的最晚时间vl
            if (vl[k] - e->weight < vl[gettop])    
                 vl[gettop] = vl[k] - e->weight;
        }
    }
    for (j = 0; j < G->n; j++)
    {
        for (e = G->adjList[j].firstarc; e; e = e->next)
        {
            k = e->adjvex;
            e = ve[j];                    //活动最早发生时间
            l = vl[k] - e->weight;        //活动最晚发生时间
            if (e == l)                    //(8)关键活动判断
            {
                printf("<v%d,v%d> lengthL%d,",
 G->adjList[k].data, e->weight);
            }
        }
    }
}

图的创建算法与上一节拓扑排序中的创建算法大同小异，只是多了一个对边上权值的赋值，这里就不再给出。在拓扑排序之前，定义了几个全局变量，用来存储求解过程中用到的信息。

对关键路径求解算法进行分析：其中包含的拓扑排序算法，时间复杂度为O(n+e)；其次的for循环，其时间复杂度为O(n)；之后的while循环，时间复杂度同样为O(n+e)；最后的双层for循环，时间复杂度仍为O(n+e)。所以，求解关键路径的算法，时间复杂度为O(n+e)。