图的邻接矩阵存储

邻接矩阵存储法中，使用一个线性表来存储图中顶点信息，使用一个邻接矩阵来存储顶点的关系，也就是边。通常使用一个一维数组和一个二维数组分别存储线性表和邻接矩阵，所以邻接矩阵存储又称作做数组表示法。

假设图G=(V,E)有n个顶点，则G的邻接矩阵A是一个n阶矩阵，其性质如下。

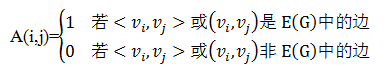
其中1表示两个顶点之间有边，0表示两个顶点之间没有边。以图7-1中的有向图G1和无向图G2为例，它们的邻接矩阵分别如图1中A1和A2所示。

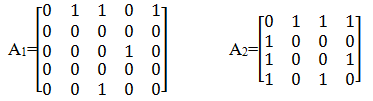
图1 图的邻接矩阵示例

假设需要存储的是一个有n个顶点的网图G=(V,E)，则可使用下面方法定义矩阵。

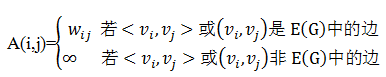
其中wij表示边上的权值， 表示一个计算机可以存储的、大于边上所有权值的、足够大的数。以图7-3中的有向图G1和无向图G2为例，它们的邻接矩阵分别如图2中A1和A2所示。

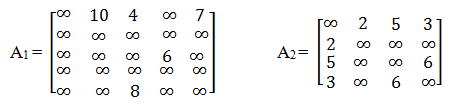
图2 网图的邻接矩阵示例

创建图的算法并不难，只要为结构中的数据一一赋值，便能完成图的创建。通常使用以下定义来描述图的结构定义。

#define MAX_VERTEX_NUM 100
typedef struct
{
  int n;   //图中顶点数目
  int e;   //图中边的数目
  //顶点存储
  int vexs[MAX_VERTEX_NUM];
  //边存储
  int edgesMAX_VERTEX_NUM;
}Graph;

这里顶点和边的数据类型以int为例，实际应用时顶点中可能存放有其它信息，读者在日后的学习中可以根据需求自行定义。

需要注意的是，在为结构体中的矩阵赋值之前需要对其中所有元素初始化，否则矩阵中可能会存储有垃圾数据，在取值时发生错误。下面使用C语言来实现创建无向图的算法。

//基于邻接矩阵的矩阵创建
void CreateMGraph(MGraph *G)
{
  int i, j, k, w;
  printf("请输入顶点数目和边的数目：");
  scanf("%d%d", &G->n, &G->e);
  //初始化邻接矩阵
  for (i = 0; i < G->n;i++)
  for (j = 0; j < G->n; j++)
​    G->edges[i][j] = INF;   //初始化为无穷大
  printf("请输入%d条边和对应权值（a b c）：\n", G->e);
  for (k = 0; k < G->e; k++)
  {
​    scanf("%d%d%d", &i, &j, &w);//输入边的信息
​    G->edges[i][j] = w;
​    G->edges[j][i] = w;
  }
}

这个算法的时间复杂度为O(n2+ n*e)，因为e<n，所以时间复杂度为O(n2)。创建有向图的代码与之基本相同，只是在为邻接表赋值时不需要为对称边进行赋值。

邻接矩阵存储法来表示图时，邻接矩阵唯一。

使用邻接矩阵来存储具有n个顶点的有向图时，矩阵所用空间为n2。对于一个具有n个顶点的无向图，所用空间为n(n-1)/2。因为无向图的邻接矩阵一定是对称的，而且主对角线一定为零（因为是简单图），所以只存储其剔除了一条对角线的上（下）三角矩阵即可。

邻接矩阵存储法可以清晰的看出图中哪两个顶点之间有边相连，很容易获得每个顶点的度：a对于有向图的顶点vi，其出度为邻接矩阵第i行中元素的个数，入度为邻接矩阵第i列中元素的个数，度为第i行和第i列元素个数之和。b对于无向图的顶点vi，其度为邻接矩阵第i行或第i列中元素的个数。

经过以上分析，可以轻松地写出图的基本操作的算法。但是因为其存储方式的问题，这些操作所花费的时间代价很大，因为要确定每个顶点的度，需要按行或列遍历矩阵中的每一个元素，而在遍历的过程中，尤其是矩阵中有值的元素较少时，算法会在空值处消耗很多时间。