克鲁斯卡尔(Krushal)算法
Prim算法是以某个顶点为起点,逐条寻找依附于当前顶点的边中权值最小的边来构建最小生成树,在此过程中将用到的顶点依次加入顶点集U中,直到U=V为止,其过程产物为图的一个连通子图。而Kruskal算法是将图的所有边依照权值排序,依次取边,直到边集TE中边的数目为n-1为止,其过程产物为图的多个连通子图。
假设当前有一无向连通网图G=(V,E),它的最小生成树为T=(U,TE)。U是顶点集V的子集,TE是边集E的子集。构造最小生成树的步骤如下:
(1)初始化顶点集U=V,即将图中所有顶点放入顶点集U;初始化边集TE为空,此时相当于图中的每一个顶点都是一个连通子图。
(2)将图中的边按照权值递增顺序依次选取,若该边未使生成树形成环路,则加入边集TE,否则舍弃,依次选取下一条边进行判断,直到边集TE中包含n-1条边为止。
使用Kruskal算法求解最小生成树,需要一个存储边集的数组E[],和记录每个顶点所在连通子图编号的数组vset[]。
数组E[]存储图中所有边的相关信息(顶点u,顶点v,权值w),其中的元素按照权值递增排序。数组vset[]中存储每个顶点所在连通子图的编号,vset[i]表示第i个顶点所在连通子图的编号,用于判断一条边的两个顶点加入生成树中是否会形成环路。构造开始时图中的各个顶点皆不相连,每一个顶点都是一个连通子图,所以vset[]中的元素初始值均不相同。
由此,需要构造边的数据结构定义,其定义如下。
//图中边的数据结构定义
typedef struct
{
int u; //起点
int v; //终点
int w; //权值
}Edge;以上一节图1中的无向网图G为例,展示使用Kruskal算法构建最小生成树的过程。其过程如下图1所示。
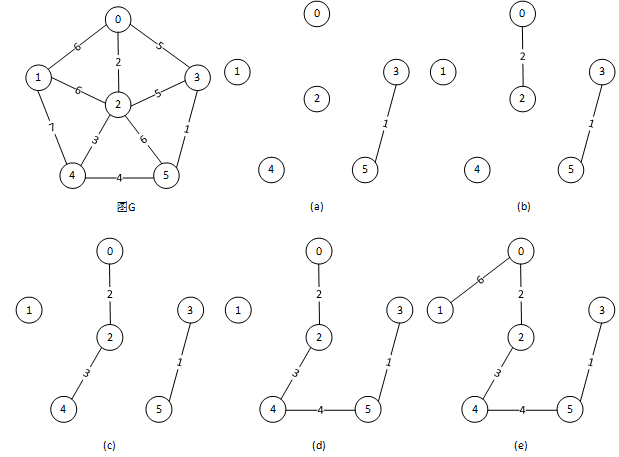
图1 Kruskal算法求解最小生成树过程
根据Kruskal算法求解步骤,在使用Kruskal算法对图G求解最小生成树时,首先初始化顶点集U=V,初始化边集TE=∅。此时每个顶点相当于一个连通子图,让每个顶点的编号作为此时辅助变量vset[]中各个连通子图的编号,则vset[6]={0,1,2,3,4,5}。
假设以邻接矩阵作为图G的存储结构,遍历图G的邻接表,将其边存入数组E[]中,并将E[]中数据按照权值递增排序,则E[10]={(3,5,1),(0,2,2),(2,4,3),(4,5,4),(0,3,5),(2,3,5), (0,1,6), (1,2,6),(2,5,6), (1,4,7)}。依次取E[10]中的边:
取E[0]={3,5,1},其中(3,5)为边,1为边上的权值。边(3,5)的顶点v3和v5在vset[]中对应的连通子图编号分别为3和5,vset[3] vset[5],所以顶点v3和v5不会形成回路,将边(3,5)加入边集数组TE中,并将所有连通子图编号为5的元素数值修改为3:这里只需修改vset[5],使vset[5]=vset[3]。此时TE={(3,5)},vset[6]={0,1,2,3,4,3}。过程产物如图1(a)所示。
取E[1]={0,2,2},其中(0,2)为边,2为边上的权值。边(0,2)的顶点v0和v2在vset[]中对应的连通子图编号分别为0和2,vset[0] vset[2],所以顶点v0和v2不会形成回路,将边(0,2)加入边集数组TE中,并将所有连通子图编号为2的元素数值修改为0:这里只需修改vset[2],使vset[2]=vset[0]。此时TE={(3,5),(0,2)},vset[6]={0,1,0,3,4,3}。过程产物图如图1(b)所示。
其后依次选取E[]中元素E[2]、E[3],并将边(2,4)、(4,5)加入边集TE中。边(2,4)加入TE后,TE={(3,5),(0,2),(2,4)},vset[6]={0,1,0,3,0,3},过程产物图如图7-21(c)所示;边(4,5)加入边集TE后,TE={(3,5),(0,2),(2,4),(4,5)},将所有vset[]值为vset[5],即vset[]中所有值为3的元素的数值修改为0,则vset[6]={0,1,0,0,0,0}。过程产物图如图1(d)所示。
之后按照求解步骤,本该选取E[4]={0,3,5},但是vset[]数组中vset[0]=vset[3]=0,选择边(0,3)会构成回路,所以我们放弃这一条边。选择下一条边E[5]={2,3,5},同样因为vset[2]与vset[3]值相等,会构成回路,所以选择放弃。
继续往后选择E[]中元素E[6]={0,1,6}。此时 vset[0]=0,vset[1]=1,vset[0] vset[1],添加边(0,1)不会构成回路,所以选定此边。添加此边后边集TE={(3,5),(0,2),(2,4),(4,5),(0,1)},vset[6]={0,0,0,0,0,0}。
到这里,边集TE中已有6-1=5条边,最小生成树构造完成,结果如图1(e)所示。
结合以上讲解,下面给出求解最小生成树的Kruskal算法。
//排序算法
void Sort(Edge E[], int e)
{
int i, j;
for (i = 0; i < e - 1; i++)
for (j = 0; j < e - i - 1; j++)
{
if (E[j].w>E[j + 1].w)
{
Edge tmp = E[j];
E[j] = E[j + 1];
E[j + 1] = tmp;
}
}
}
//克鲁斯卡尔算法求解最小生成树
void Kruskal_MinTree(MGraph *G)
{
int i, j, u1, v1, sn1, sn2, k;
int vset[MAX_VERTEX_NUM]; //存放下标对应的顶点所属的连通子图编号
Edge E[MAX_EDGE_NUM]; //存放图G中的所有边
k = 0;
//将图转化为边集数组
for (i = 0; i < G->n; i++)
for (j = 0; j < i + 1; j++)
{
//遍历邻接矩阵,并将存在的权值存入边集数组E[]
if (G->edges[i][j] && G->edges[i][j] != INF)
{
E[k].u = i;
E[k].v = j;
E[k].w = G->edges[i][j];
k++;
}
}
//排序
Sort(E, k); //排序算法:将边集E中的元素按权值大小升序排列
for (i = 0; i < G->n; i++)
vset[i] = i; //初始化vset[]数组,每个顶点相当于一个连通子图
k = 1; //记录已加入生成树中的边的数目
j = 0; //E中边的下标,从0开始
//寻找合适的边
while (k < G->n)
{
u1 = E[j].u;
v1 = E[j].v;
sn1 = vset[u1]; //分别得到一条边两个顶点所属的集合编号
sn2 = vset[v1];
if (sn1 != sn2)
{
//两个顶点属于不同集合,该边可以作为最小生成树的一条边
printf("(%d,%d):%d\n", u1, v1, E[j].w);
k++; //边计数加一
for (i = 0; i < G->n; i++)
if (vset[i] == sn2) //统一两个集合的编号
vset[i] = sn1;
}
j++; //扫描下一条边
}
}Kruskal算法中涉及排序,在后面的章节会详细讲解,此时只需要知道它的作用是将边集数组E[]中的数据按照权值的大小递增排序,它的时间复杂度为O(n2)即可。需要重点掌握的是该算法如何在边集数组中找到合适的边,这一部分算法包含在while循环中。while循环从e条边中寻找n-1条边,最坏情况执行e次,其中的for循环执行n次,因为while循环的时间复杂度为O(n2+e),对于连通无向图,e>(n-1),所以使用克鲁斯卡尔算法构造最小生成树的时间复杂度为O(n2)。
