普里姆(Prim)算法
假设当前有一无向连通网图G=(V,E),它的最小生成树为T=(U,TE)。U是顶点集V的子集,TE是边集E的子集。若要求G的T,需要任意选定V的一个顶点,初始化 ,以v到其它(n-1)个顶点的所有边为侯选边,重复执行以下步骤:
,以v到其它(n-1)个顶点的所有边为侯选边,重复执行以下步骤:
(1)从侯选边中挑选权值最小的边加入TE,设该边在V-U中的顶点是k,将k加入U中。
(2)考察当前V-U中的所有顶点m,修改侯选边,若边(k,m)的权值小于原来和顶点m关联的侯选边,则用边(k,m)取代后者作为侯选边。
直到U=V为止。
在这个过程中,需要两个辅助变量,记录从U到V-U之间具有最小代价的边。这两个辅助变量分别为adjvex[n]和lowcost[n](n为顶点个数),对于每个顶点v V-U,变量adjvex[v]存储该边依附的、存在于U中的顶点,变量lowcost[v]域存储该边上的权值。下面以图1中的无向网图G为例,使用Prim算法构造一棵最小生成树。
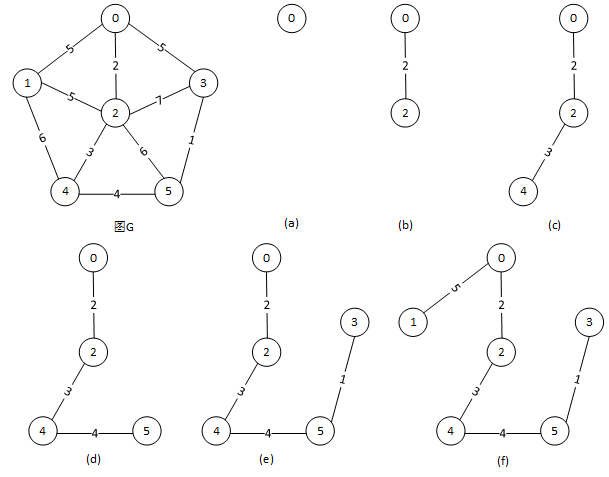
图1 Prim算法求解最小生成树过程
在对图1中的图G求解之前需要先对辅助变量进行初始化。用1代表与当前顶点对应的顶点之间有边,0代表没有边,那么adjvex[6]={0,0,0,0,0,0}(初始化时将数组adjvex[]中元素初始化为0,但是为了区分顶点v0,用“-”代替非顶点的0(初始化的0和数值重归于0))。选取一个足够大的值来初始化辅助变量lowcost[],假设这个值为65535,那么lowcost[6]= { 65535, 65535, 65535, 65535, 65535, 65535},在求解过程中lowcost[]元素值可能出现这些情况:
(1)若lowcost[v]=0,则顶点v∈U,表示该顶点已经被加入生成树;
(2)若lowcost[v]=65535,表示尚未出现依附与该顶点的边;
(3)若0<lowcost[v]<65535,表明出现过依附于该顶点的边,此时若有依附于该顶点的新边出现,且边上的权值小于当前lowcost中记录的权值,那么应当更新lowcost[v]的值。
因为邻接矩阵可以清晰地看出各个顶点与其它顶点之间的关系,并能表示边上的权值,所以在这里给出邻接矩阵。当辅助数组的数据需要更新的时候,可以根据顶点编号查看对应行的邻接矩阵数据。图G的邻接矩阵如下:

下面给出使用Prim算法求解最小生成树的过程:
任意选定顶点v0作为起始顶点,观察依附于v0的边及其权值。对应的过程为图7-20(a)。此时顶点集U={v0},边集TE为空。在此期间需要修改辅助变量的值。顶点v0与顶点v1、v2、v3之间有边,所以将数组adjvex[6]对应下标为1、2、3的元素修改为0,表示此处存在依附与顶点v0的边。修改之后的数组为:adjvex[6]={-,0,0,0,-,-};边的权值小于当前lowcost数组中对应值时,需要修改数组中的值,修改后的lowcost数据为:lowcost[6]={0,5,2,5, 65535,65535}。
因为边(v0,v2)上的权值最小,所以选定边(v0,v2),将边依附的另一个顶点v2加入集合U,将边(v0,v2)加入集合TE。此时集合的值分别为:U={v0, v2},TE={(v0,v2)}。对应的过程为图1(b)。
之后为重复操作的步骤:
观察依附于v2(上述步骤中加入顶点集U的顶点)的边及其权值。并修改辅助变量的值:因为边(v2,v1)与边(v2,v3)上的权值大于边(v0,v1)与边(v0,v3)的权值,所以adjvex中仍然记录顶点v0,修改后的数组为:adjvex[6]= {-,0,-,0,2,2},lowcost[6] ={0,5,0,5, 3, 6}。
其中权值最小的边为(v1,v4),对应的权值为3。将顶点v4加入顶点集U,边(v2,v4)加入边集TE。此时集合的值分别为:U={v0,v2,v4},TE={(v0,v2),(v2,v4)}。对应的过程为图1(c)。
观察依附于v4的边及其权值,修改辅助变量的值:adjvex[6]= {-,0,-,0,-,4}, lowcost[6]={0, 5, 0,5,0,4},其中权值最小的边为(v4,v5),将顶点v5加入集合U,边(v4,v5)加入集合TE。
其次按照算法执行与顶点v2、v4相同的步骤,依次选中顶点v3、v1,和对应的边(v5,v3)、(v0,v1)。此时顶点集和U=V,最小生成树构造完毕。
表1中给出了构造过程中辅助变量的变化过程,以及每一步选定的数据,读者可以参考图1与上述步骤,结合表1来理解Prim算法的基本思想。
表1 顶点选择与变量变化过程
| 顶点v | lowcost[] | 选中的边:权值 | adjvex[] |
|---|---|---|---|
| 1 | lowcost[6]={0,4,2,5,65535,65535} | (0,2):2 | adjvex[6]={-,0,0,0,-,- } |
| 3 | lowcost[6]={0,5,0,5,3,6} | (2,4):3 | adjvex[6]={-,0,-,0,2,2} |
| 5 | lowcost[6]={0,5,0,5,0,4} | (4,5):4 | adjvex[6]={-,0,-,0,-,4} |
| 6 | lowcost[6]={0,5,0,1,0,0} | (5,3):1 | adjvex[6]={-,0,-,5,-,-} |
| 4 | lowcost[6]={0,5,0,0,0,0} | (0,1):5 | adjvex[6]={-,0,-,-,-,-} |
| 2 | lowcost[6]={0,0,0,0,0,0} | adjvex[6]={-,-,-,-,-,-} |
在顶点v3进入集合U之时,v3的邻接点已经全部进入U,此时选择的边定然不再依附于v3,因此从adjvex[]数组获得一条边:该边依附的其中一个顶点为其对应元素下标1,另一个顶点为adjvex[1]中存储的元素0。从lowcost[]数组获得该边对应的权值:lowcost[]数组中对应adjvex[1]的权值为lowcost[1]=5。所以选定的边及其权值为(v0,v1):5。
通过以上分析可知,adjvex[]数组中存储的数据与该元素对应的下标构成一条边,lowcost[]数组中存储的数据对应adjvex[]数组中相应位置的边的权值。
结合以上讲解,下面给出Prim算法求解最小生成树的算法。
//Prim算法求解最小生成树
void Prim_MinTree(MGraph *G)
{
int min, i, j, k;
int adjvex[MAX_VERTEX_NUM]; //保存相关顶点下标
int lowcost[MAX_VERTEX_NUM];//保存相关顶点间边的权值
lowcost[0] = 0; //初始化边(0,0)权值为0,即v0加入生成树
//lowcost的值修改为0
//就表示该下标的顶点已加入生成树
adjvex[0] = 0; //选取顶点v0为起始顶点
for (i = 1; i < G->n; i++) //循环遍历除v0外的全部顶点
{
lowcost[i] = G->edges[0][i]; //将v0顶点与其邻接点边上的权值存入数组
adjvex[i] = 0; //adjvex[]初始化为顶点v0的编号0
}
for (i = 1; i < G->n; i++)
{
min = INF; //初始化最小权值为无穷大
j = 1;
k = 0;
while (j < G->n) //遍历全部顶点
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
//如果权值w满足0<w<min
min = lowcost[j]; //则让当前权值成为最小值
k = j; //若边的权值修改,将对应顶点下标存入k
}
j++;
}
printf("(%d,%d)", adjvex[k], k); //打印当前顶点边中权值最小的边
lowcost[k] = 0; //将当前边中选中的边权值置为0
//表明该下标的顶点已加入生成树
for (j = 1; j < G->n; j++)
{
//依附顶点k的边权值小于此前尚未加入生成树的边的权值
if (lowcost[j] != 0 && G->edges[k][j] < lowcost[j])
{
//则用较小的权值替换lowcost[]中的权值
lowcost[j] = G->edges[k][j];
//并将adjvex[]中对应位置的元素修改为新的依附顶点
adjvex[j] = k;
}
}
}
}该算法的循环嵌套很清晰,第一个for循环的时间复杂度为O(n),第二个for循环外层时间复杂度为O(n),内层嵌套了两个并列的循环,时间复杂度都为O(n)。所以这个算法的时间复杂度为O(n+n*
(n+n)),即O(2n2+n),也就是O(n2)。
