什么是最小生成树

1、图的连通性问题

在前面小节中学习过的针对无向图的连通、连通分量、连通图，针对有向图的强连通、强连通分量这些概念是本小节学习的基础。

上一节针对遍历算法的学习中也有提到连通性问题。dfs算法和bfs算法都是针对连通图的，如果是非连通图，需要根据各自连通分量的数量调用相应次数的遍历算法，假如一个非连通图有3个连通分量，那么需要调用3次遍历算法才能走遍该图中所有顶点。每调用一次，已访问的顶点与相关的边就构成图的一个连通分量。

如果第一次调用遍历算法之后状态数组visited[]中便不存在未被访问的顶点，那说明这个图是一个连通图；如果有，说明是一个非连通图。比如图7-4中的非连通无向图G，其遍历结果为两个顶点集：V1(G)={A,B,D,E}，V2(G)={C,F}。这两个顶点集也恰好是G中两个连通分量的顶点集。

上一节中给出的是针对一个连通分量或者说是一个连通图的遍历算法，要实现非连通图的遍历，需要一个简单的函数实现对dfs或者bfs算法调用。函数实现如下。

//非连通图的遍历算法实现
void connected(Graph G)
{
  int i;
  for (i = 0; i < G.n; i++)   //遍历顶点数组
  {
​    if (visited[i] == 0)    //判断顶点i的访问状态
​    {
​      DFS(G, i);       //未访问则调用遍历算法
​      printf("\n");
​    }
  }
}

显然该函数的时间复杂度和遍历算法的时间复杂度相同。

2、最小生成树的概念

前面章节中已经讲解了生成树的概念：一个连通图的生成树，是包含了该连通图全部顶点的一个极小连通子图。顶点数目为n的连通图的生成树，必定具有n个顶点和n-1条边。为生成树上任意添加一条原图中存在的边，将会构成回路。不同的遍历算法会产生不同的生成树。

加权图生成树的代价是指该生成树所有边的权值之和。对于一个带权图，它的生成树可能不唯一，这些生成树的权值之和也可能不尽相同，最小生成树，就是指所有生成树中权值之和最小的那一棵（或多棵）。

所以，一棵最小生成树满足下列条件：

(1) 这是一棵生成树；

(2) 这棵生成树的权值之和是所有生成树中最小的。

假设现在有一个无向连通图G，图G有n个顶点。如果T是无向连通图G的一棵最小生成树，那么它包含以下性质：

(1) 包含图G中的所有顶点，即它必定有n个顶点；

(2) 包含图G中的n-1条边；

(3) 不包含回路。若为T任意添加一条图G中存在而T还不包含的边，T中将会构成回路；

(4) T是图G所有生成树中权值之和最小的那棵。

3、最小生成树的应用

以一个城市的通讯线路搭载为例。假设现在有8个城市，政府计划在这8个城市之间搭载通讯线路，现已估算出8个城市每条可行线路搭载所需花费的代价，将每个城市简化为一个顶点，将两个城市之间所需代价作为顶点之间边上的权值，以一个无向图G来代表城市线路规划模型。图G如图1所示。

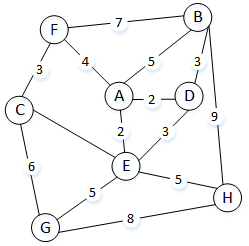
图1 城市线路规划图G

保证通讯畅通是第一要素。要保证两两之间能够通讯，只要保证两个顶点之间有路径即可。根据生成树的概念可知：需要在规划图G的所有边中选中7条，这7条线路可以链接起这8个城市。图2中给出了一些方案，这些方案都是图G的生成树。

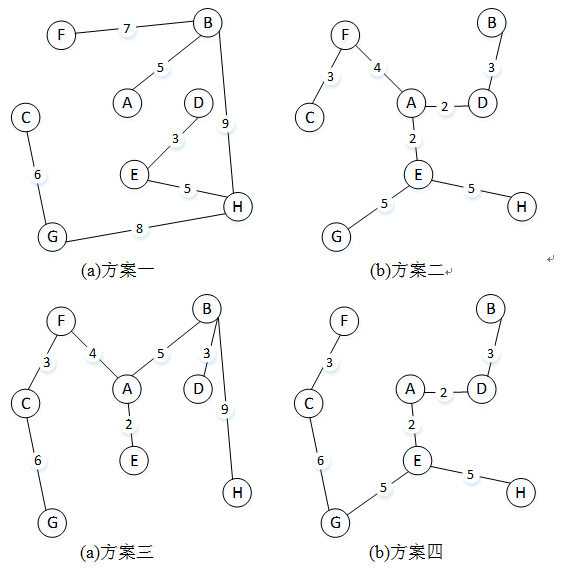
图2 规划方案

图中的边有很多，随便就能规划出几种方案，但是哪种方案才是最优的呢？通讯网络的搭建伴随着财力、物力、人力等等的消耗，通常最需要关注的第二个因素就是花费。根据图2中这四种方案各条线路上的权值，分别计算出这些方案所需的花费：

方案一：7+5+9+3+5+6+8=43

方案二：3+4+3+2+2+5+5=24

方案三：3+4+5+2+3+6+9=32

方案四：3+6+5+2+2+3+5=26

通过计算结果可以看出，方案一的花费几乎是方案二的两倍，方案四又比方案二要多消耗一些。如何才能得到即能连通所有城市，又能将花费控制在最低的线路图呢？这正是一个需要使用最小生成树思想的实例。图2中的方案二是规划图G 的一棵最小生成树。

那么究竟如何构造一棵最小生成树呢？通常使用普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法这两种算法求解。