每对顶点的最短路径
在一些情境中,起点和终点可能都不固定。例如依然是家、学校、商场、公园等等这些地点,在不同的时间我们可能处在不同的地点,随后有可能去往其它任一地点,这样就需要对每两个地点之间的最短路径求解。同样将每个地点抽象为一个顶点,这样的问题就转化为求图中每对顶点之间最短路径的问题。
两个顶点之间的最短路径不外乎两种情况,以顶点vi和顶点vj之间的路径为例:一是vi与vj之间有边直接相连,也就是有直接路径,那么两点之间的路径长度即边(vi,vj)的权值;二是从顶点vi到顶点vj经过顶点vk(k>1,k +),其路径为(vi, vk, vj)。
在上小节学习的基础上求解此问题时,很容易想到:让每个顶点作为源点,调用Dijkstra算法循环n遍,便可求出每对顶点的最短路径。使用Dijkstra算法求解此问题的时间复杂度为O(n3)。
本节讲解一个新的算法——弗洛伊德(Floyd)算法。
Floyd算法的基本思想是:假设dist[i][j]为顶点vi到顶点vj的最短距离,对于每一个顶点vk(0 k n-1),检查dist[i][k]+dist[k][j]<dist[i][j]是否成立,如果成立,说明以vi为源点,经过顶点vk到达vj比从vi直接到vj的路径更短,使dist[i][j]=dist[i][k]+dist[k][j]。这样一来,当迭代完所有顶点vk(0 k n-1),dist[i][j]中记录的便是顶点vi到vj的最短路径长度。Floyd算法又形象地称为点插法,如图1所示。
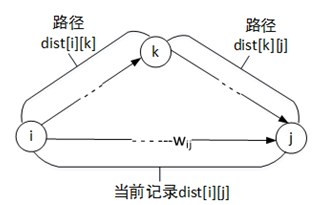
图1 插入点vk构成新路径
另外用二维数组path[][]存储最短路径,当顶点vk(0 ≤k≤n-1)从v0到vn-1迭代完毕时,path[i][j]中存储从顶点vi到顶点vj最短路径中顶点vj的前一个顶点编号,这点与Dijkstra算法中path[]的存储方式相同。初始时,若弧<vi,vj>存在,path[i][j]=i,否则,path[i][j]= -1。
以图2中的有向网图G为例,使用二维数组存储每对顶点间的最短路径dist[i][j],path[i][j]存储当前路径上顶点vj的前一个顶点。因为图G有4个顶点,所以插入四次即可。下面用矩阵dist0~3 、path0~3分别表示迭代时插入不同顶点后的矩阵,矩阵中显示更新后的路径长度和路径上当前顶点对应的前一个顶点。

图2 有向图G与初始的dist[][]、path[][]
图2中的矩阵存储了原始的dist和path数组,是图G中顶点与边状态的初始化。其中边(i,i)的路径长度设置为0,前置顶点设置为i。若两顶点直接相连,矩阵dist中的数据为边上权值,若无直接相连的边,dist中的数据设置为一个足够大的值,图示中用无穷大表示。
下面采用Floyd算法求解最短路径。针对每一组顶点vi和vj,判断dist[i][j]>dist[i][0]+dist[0][j]是否成立,若成立则修改dist[i][j],使dist[i][j]= dist[i][0]+dist[0][j]。后面的求解过程中,更新后的dist与path分别如矩阵disti和pathi所示(0 。disti中带的数据表示修改后的距离,pathi中带的数据表示新加入到最短路径上的顶点。
首先考虑顶点v0。加入顶点v0后,dist[2][1]、dist[2][3]、dist[3][1]由原来的无路径变为有路径,修改dist和path中存储的数据,修改后的结果如矩阵dist0和path0所示。

其次考虑顶点v1,在已经更新过的最短路径长度矩阵dist0和前置顶点矩阵path0的基础上,插入顶点v1,dist[0][2]的路径变为v0->v1->v2,路径长度从7更新为4,前置顶点path[0][2]值修改为1。修改后的结果如矩阵dist1和path1所示。
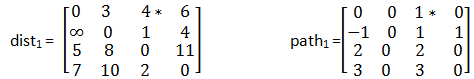
随后以最新的最短距离矩阵dist1和前置顶点矩阵path1为基础,考虑顶点v2。加入顶点v2后,dist[1][0]由不存在变为v1->v2->v0,路径长度为6,path[1][0]的前置顶点修改为2。修改后的结果如矩阵dist2和path2所示。
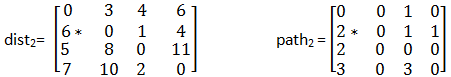
最后以dist2和path2为基础,考虑顶点v3。加入顶点v3后,经过比较,没有任何路径需要修改,所以dist3=dist2,path3=path2。
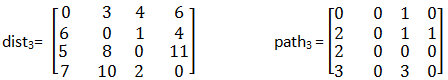
此时得到最终结果,求得的最短路径长度矩阵如图3中的dist所示,各顶点的前置顶点矩阵如图3中的path所示:
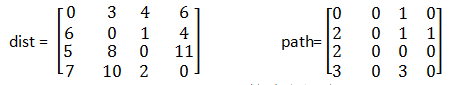
图3 Floyd算法求解结果
Floyd算法通常使用一个简单的三层循环来实现。外面两层循环分别确定顶点vi和vj,第三层循环用来不断更换插入的顶点,比较路径权值并依据实际情况更新。其时间复杂度也为O(n3)。虽然与Dijkstra算法时间复杂度相同,但是其代码简洁优雅,易于理解。
下面给出Floyd算法求解最短路径的代码实现。
//输出每对顶点之间的最短路径
void Dispath(MGraph *G, int dist[MAX_VERTEX_NUM][MAX_VERTEX_NUM],
int path[MAX_VERTEX_NUM][MAX_VERTEX_NUM])
{
int i, j, k, s;
int apath[MAX_VERTEX_NUM], d; //存放一条最短路径中间顶点及其顶点个数
for (i = 0; i < G->n; i++)
{
for (j = 0; j < G->n; j++)
{
if (dist[i][j] != INF && i != j) //若vi与vj之间存在路径
{
printf("从%d到%d的路径为:",i, j);
k = path[i][j];
d = 0;
apath[d] = j; //路径上添加终点
while (k != -1 && k != i) //插入中间点vk
{
d++;
apath[d] = k;
k = path[i][k];
}
d++;
apath[d] = i; //路径上添加起点
printf("%d", apath[d]); //输出起点
for (s = d - 1; s >= 0; s--) //输出路径上的中间顶点
printf(",%d", apath[s]);
printf("\t路径长度为:%d\n", dist[i][j]);
}
}
}
}
//Floyd算法求解每对顶点的最短路径
void Floyd(MGraph *G)
{
int dist[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
int path[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
int i, j, k;
for (i = 0; i < G->n; i++)
{
for (j = 0; j < G->n; j++)
{
dist[i][j] = G->edges[i][j];
if (i != j&&G->edges[i][j] < INF)
path[i][j] = i; //顶点vi到vj有边时
else
path[i][j] = -1;
}
}
for (k = 0; k < G->n; k++)
for (i = 0; i < G->n; i++)
for (j = 0; j < G->n; j++)
if (dist[i][j]>dist[i][k] + dist[k][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = path[k][j]; //修改最短路径
}
Dispath(G, dist, path); //输出最短路径
}上文的代码包含输出最短路径的Dispath()函数和Floyd算法。这里的Dispath()函数与Dijkstra算法中调用的Dispath()函数大同小异,因此主要来看Floyd算法。Floyd算法包含两个并列for循环,第一个for循环为双层循环,主要用于初始化dist[][]数组和path[][]数组,时间复杂度为O(n2);第二个for循环为三层循环,是Floyd算法的核心内容,其时间复杂度为O(n3)。综上分析,Floyd算法的时间复杂度为O(n3)。
