平衡二叉树的插入

在平衡二叉树中插入结点要随时保证插入后整棵二叉树还是平衡的，但是由上一节的学习我们知道在插入结点时往往会破坏二叉树的平衡性，如上一节图2中所示，会产生不平衡子树。因此为了保证插入结点后二叉树仍是平衡的，就需要找出插入新结点后失去平衡的最小子树根结点。然后再调整这棵子树中有关结点之间的链接关系，使之成为新的平衡子树。当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。调整结点之间的链接关系的基本方法就是旋转，也有书籍称之为结点交换。

旋转的方式有右旋转、左旋转、左右旋转、右左旋转，接下来我们用一组数据构建一棵平衡二叉树，在构建过程中讲解如何用旋转来调整二叉树的平衡。

假设有一组数据int arr[10] = {90,66,65,98,100,88,105,102,110,103 }；现在要用这组数据来构建一棵平衡二叉树，以90为根结点，下一个数据66小于90，则为它的左孩子，此时两个结点构成的二叉树是一棵平衡二叉树；然后插入结点65，65小于66，则为66的左孩子，如图1所示。

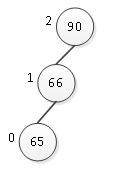
图1 前三个结点

结点左边是每个结点的平衡因子，当插入结点65后，结点90的平衡因子变为2，此树不再是

平衡二叉树，那么为了保持树的平衡性就要对树进行调整，即进行旋转。在进行旋转时也有一定的规则：在产生的最小不平衡子树的根结点及其左孩子平衡因子都为正，即在最小不平衡子树根结点的左孩子的左孩子处插入结点，则以根结点的左孩子为支点进行右旋转。图1中，66为根结点90的左孩子，而结点65就是插入到了结点66的左孩子处，根结点90与左孩子结点66的平衡因子都同为正，因此要调整二叉树的平衡就以66为支点进行右旋转，如图2所示。

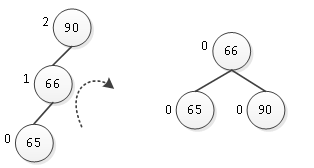
图2 右旋转

旋转之后二叉树变为以66为根结点，65和90分别为左右孩子的平衡二叉树。

接着再插入结点98，则98会成为结点90的右孩子，如图3所示。

图3 插入结点98

插入结点98之后并没有打破二叉树的平衡性，因此不需要调整。接下来再插入结点100，则100为98的右孩子，如图4所示。

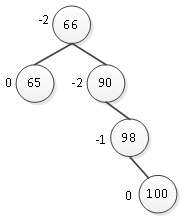
图4 插入结点100

插入结点100后打破了二叉树的平衡性，产生的最小不平衡子树以90为根结点。此时要调整

树的平衡性，但是此次插入结点是在90右孩子的右孩子98处插入，结点90及其右孩子平衡因子都为负，因此需要左旋转。左旋转规则为：在产生的最小不平衡子树根结点右孩子的右孩子处插入结点，即最小不平衡子树的根结点及其右孩子的平衡因子都为负，则以根结点的右孩子为支点进行左旋转，根结点变为支点的左孩子。图4中的二叉树，即以结点98为轴左旋转，将结点90变为其左孩子，如图5所示。

图5 左旋转

左旋转之后，结点98变为了66的右孩子，结点90变为了结点98的左孩子，整棵树又恢复了平衡。需要注意的是如果插入结点不是98的右孩子而是其左孩子，例如插入的结点值为97，如图6所示。

图6 结点100换成97

这样如果直接进行简单的左旋转，则97会成为98的右孩子，就不符合二叉排序树的性质，因此不能简单的直接左旋转。仔细观察会发现结点90与结点98的平衡因子符号不同，因此不能简单旋转。在旋转之前可以先将两者符号统一，先对结点98与97进行右旋转，使98成为97的右孩子，如图7所示。

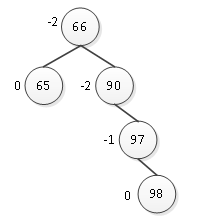
图7 旋转结点98与97

这样就与图5所示二叉树平衡性一样，此时可以直接进行左旋转，如图8所示。

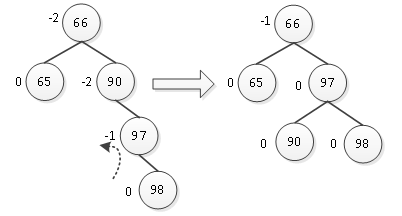
图8 左旋转

​ 此处为将100用97替换所出现的情况，如果在插入过程中出现平衡因子符号不同的情况，读者也要知道如何处理。

接下来插入结点88，则88会成为90的左孩子，如图9所示。

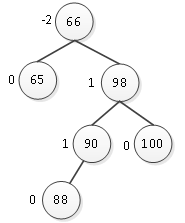
图9 插入结点88

插入结点88之后，也打破了树的平衡性，产生的最小不平衡子树以66为根结点。66的平衡因子为负，其右孩子98的平衡因子为正，两者符号不同，因此旋转方式也会改变。先要取消平衡因子符号的差异，当产生的最小不平衡子树中，从根结点的插入路径为右->左->左时，先要以此根结点的右孩子的左孩子为支点进行右旋转，然后再进行左旋转。在图8-24中，产生的最小不平衡子树以66为根结点，则从66到插入的结点88的路径就是为右->左->左，那么就先绕结点90（它为根结点66右孩子的左孩子）进行右旋转，如图10所示。

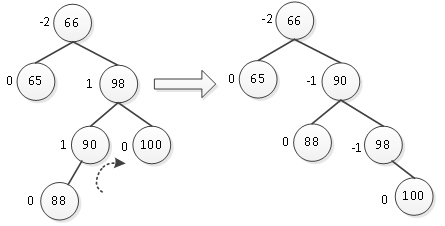
图10 右旋转后

经过右旋转之后，结点66与结点90的平衡因子符号相同，此二叉树的平衡情况与图4有些

类似，最小不平衡子树的根结点与其右孩子的平衡因子都为负，按照规则绕结点90进行左旋转，结点66变为90的左孩子，结点88变为66的右孩子，如图11所示。

图11 左旋转

插入结点88，根据插入的位置及平衡因子先进行右旋转再进行左旋转，调整树的平衡。

接下来插入结点105，105为100的右孩子，生成的最小不平衡子树以98为根结点，根结点

与其右孩子平衡因子同为负，则绕结点100进行左旋转来调整二叉树的平衡性，如图12所示。

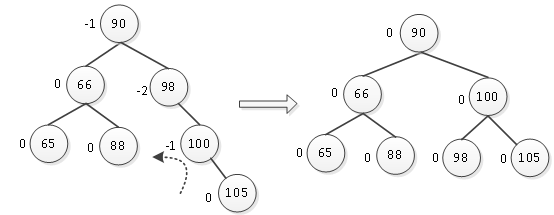
图12 插入结点105后进行左旋转

接下来插入结点102， 102为105的左孩子，如图13所示。

图13 插入结点102

插入结点102后并没有破坏二叉树的平衡性。继续插入结点110， 110为105的右孩子，

如图14所示。

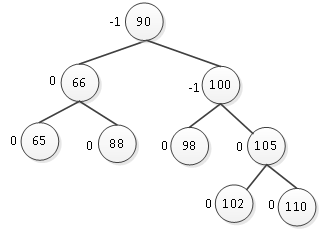
图14 插入结点110

插入结点110也没有破坏树的平衡性，因此不必调整。接下来插入结点103，则103为102的右孩子，如图15所示。

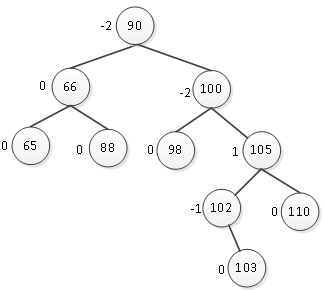
图15 插入结点103

插入结点103后，产生的最小不平衡子树以100为根结点，结点100的平衡因子为-2，结点105

的平衡因子为1，平衡因子符号不统一，与图8-24到8-26的情形有些类似。那么首先要消除平衡因子间符号的差异，绕结点102右旋，如图16所示。

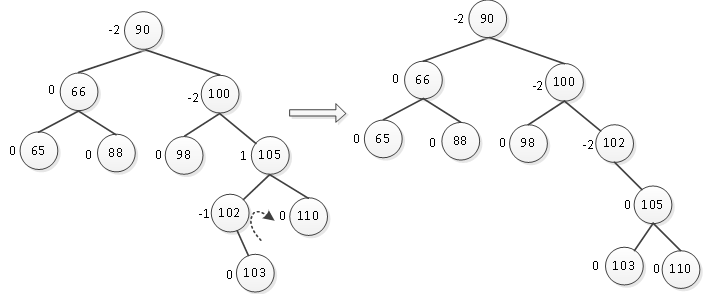
图16 绕结点102右旋

绕结点102右旋转之后得到右边的二叉树，此时再绕结点102左旋转来调整树的平衡性，如图17所示。

图17 绕结点102左旋

经过左旋转之后，得到右边的二叉树，它已经是平衡的，至此用这一组数据构建一棵平衡二叉树完成。

在构建的过程中插入结点时要随时保持树的平衡性，通过上面的学习讲解可知，大体就是分三种情况：插入结点后，如果最小不平衡子树根结点与其孩子平衡因子同为正则直接右旋；，如果最小不平衡子树根结点与其孩子平衡因子同为负则直接左旋；，如果最小不平衡子树根结点与其孩子平衡因子符号不同，则先对孩子结点进行旋转，使平衡因子符号无差异，再进行反向旋转。