平衡二叉树的删除

平衡二叉树的删除也涉及到删除后的连接问题。其删除一般分为四种情况：

● 删除叶子结点；

● 删除左子树为空右子树不为空的结点；

● 删除左子树不为空右子树为空的结点；

● 删除左右子树都不为空的结点。

删除叶子结点很简单，直接删除即可，此处不再赘述，接下来我们分别来学习一下其他三种删除情况。

1、左子树为空，右子树不为空

以图1中的平衡二叉树为例。

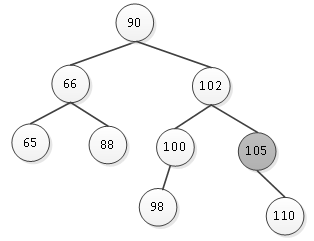
图1 平衡二叉树

现在要删除结点105，结点105有右子树没有左子树，则删除后，只需要将其父结点与其右

子树连接即可，如图2所示。

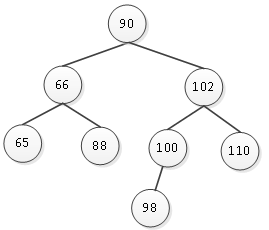
图2 删除结点105后

删除结点会使相应子树的高度减小，可能会导致树失去平衡，如果删除结点后使树失去了平衡，要调整最小不平衡树使整棵树达到平衡。删除与插入一样，在删除的过程中要时刻保持树的平衡性。

2、左子树不为空，右子树为空

要删除一个结点，结点有左子树没有右子树，这种情况与上一种情况相似，只需要将其父结点与其左子树连接即可，例如要删除图2中的结点100，其删除过程如图3所示。

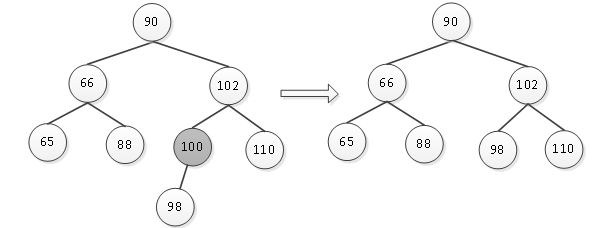
图3 删除结点100

3、左右子树均不为空

如果要删除的结点既有左子树又有右子树，则要分情况进行讨论。

（1）如果该结点x的平衡因子是0或者1，找到其左子树中具有最大值的结点max，将max内容与x的元素值进行交换，则max即为要删除的结点。由于树是有序的，因此找到的max结点只可能是一个叶子结点或者一个没有右子树的结点。

例如现在有一棵平衡二叉树，如图4所示。

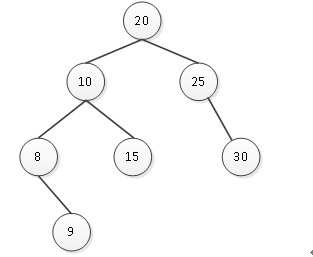
图4 平衡二叉树

现在要删除结点20，结点20的平衡因子是1，则在其左子树中找到最大结点15，将两个结点

的数据值互换，如图5所示。

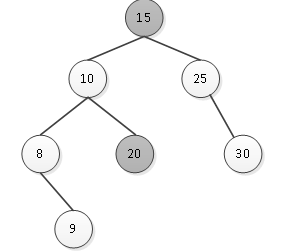
图5 结点数据值互换

然后删除结点，如图6所示。

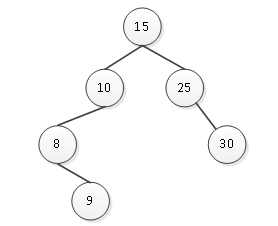
图6 删除结点20

在删除结点20之后，平衡二叉树失去了平衡，结点10的平衡因子为2，则需要对此最小不平衡二叉树进行调整，此次调整类似于插入，先进行一次左旋再进行一次右旋即可，调整后的结果如图7所示。

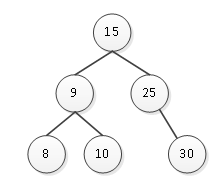
图7 调整后的平衡二叉树

（2）如果要删除的结点其平衡因子为-1，则找到其右结点中具有最小值的结点min，将min与x的数据值进行互换，则min即为新的要删除的结点，将结点删除后，如果树失去了平衡则需要重新调整。由于平衡二叉树是有序的，因此这样找到的结点只可能是一个叶子结点，或者是一个没有左子树的结点。

至此，关于平衡二叉树的基本操作已经讲解完毕。平衡二叉树的查找过程与二叉

排序树查找过程完全相同，因此，在平衡二叉树上进行查找时关键字的比较次数不会超过平衡二叉树的深度。平衡二叉树的查找复杂度为O(log2n)。