B树的概念

在具体讲解之前，读者先要弄清楚一个概念，B树即为B-树，因为B树的英文名称为B-tree，

在直译过来时就是B-树，这就让很多人产生误解，以为B树是一种树而B-树又是一种树，其实两者是同一个概念。

B树是为磁盘或其他外存设备而设计的一种多叉平衡查找树，因此它也叫多路平衡查找树，在读取外存文件时许多数据库系统都使用B树或者B树的各种变形结构，如B+树，B*树。

一棵m阶的B树（注意m阶的树并不是简单的有m个叉树）或者是一棵空树，或者在定义中要满足以下要求：

（1） 树中每个结点最多有m棵子树（m>=2）；

（2） 根结点至少有两个子结点；

唯一的例外是B树是一棵空树，根结点就是叶子结点；

（3） 除根结点外，结点中关键字的个数取值范围为(m/2) -1到m-1；（m/2向上取整）

（4） 所有叶子结点都在同一层；

（5） 除根结点和叶子结点外，如果结点有k-1个关键字，那么这个结点就有k个子结点，关键字按递增次序排列；

单纯的定义讲解理解起来会有些困难，因此以图1所示的B树为例讲解这些定义项的含义。

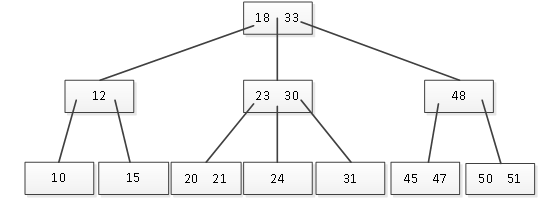
图1 B树

图1中的树是一棵B树（为了更清晰的表示关键字之间的间隔，用方框来代替圆表示结点），而且是一棵阶为3（m = 3）的B树，即一个结点最多可以有3棵子树，在此B树中，每个结点中关键字的个数取值范围为[⌈m/2⌉-1,m-1]，即[1，2]，即每个结点中最少有一个关键字，最多有两个关键字，有两个关键字就有三个孩子，有的教材也把它特殊化为2-3树。

除了根结点和叶子结点外，树中每个结点至少有2（m/2=3/2，向上取整为2）个子结点；所有叶子结点都在同一高度。在B树中，每一个结点可以存储若干个（最多为m-1）关键字，当一个结点中存储有k个关键字时，那么它会有k+1个子结点，例如根结点有18和33两个关键字，则根结点有3个子结点，这些子结点中的关键字是递增排列的，而且关键字18左边的指针指向的孩子结点中的关键字都小于18，18和33之间的指针指向的子结点中关键字处于18和33之间，33右边的指针指向的子结点中关键字的值都大于33。

​ B树适用于外存文件设备的动态索引查找，它把相关记录都放在同一个磁盘页中，从而利用了访问局部性原理。在B树的结点中没有重复的关键字，父结点中的关键字是其子结点的分界，例如根结点中的18和33两个关键字将其孩子分为三段，18和33是这三个段的界线。而且B树保证树中至少有一定比例的结点是满的。B树的这些性质能够改进空间的利用率，减少检索和更新操作的磁盘读取数目。

​ B树的结点结构如下所示：

struct BitNode
{
  int keyNum; //实际关键字个数
  struct BitNode* parent; //指向父结点的指针，可有可无
  struct BitNode* ptr; //指向子树的指针
  KeyType *key; //关键字向量：key[0]、key[1]...key[keyNum - 1]
};

​ 关于B树的结点结构读者了解即可，我们并不实现它，主要是学习它的查找、插入、删除等操作原理。

​ 在B树中查找数据时主要分为两步：

（1）把根结点读出来，在根结点所包含的关键字k1、k2….kj中查找给定的关键字值（当结点包含的关键字值不多时，可用顺序查找；当结点包含的关键字数目较多时可用折半查找），找到则查找成功；

（2）否则，确定要查找的关键字值的大小范围，根据指针指向的子结点，在子结点中继续查找。如果查找到叶子结点仍未找到，表示查找失败。

例如在图1的B树中查找值31，则先读取根结点，在根结点中有18和33两个关键字，没有值31；但可以确定31在18和33之间，因此根据指针指示读取18-33范围之间的子结点，如图2所示。

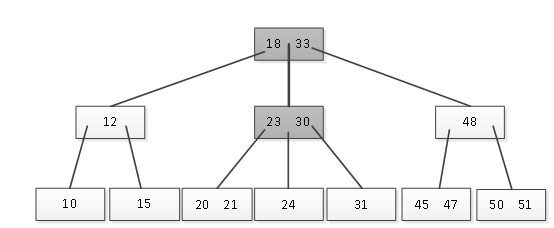
图2 由根结点读取子结点

在此子结点中查找是否存在31，结果不存在；但是确定31大于此子结点中的最大关键字30，因此接下来读取此子结点最右边的子结点，如图3所示。

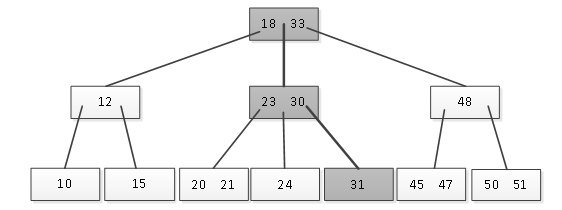
图3 由子结点读取下一个子结点

在这个子结点中只有一个关键字31，与待查找关键字相等，查找成功。本次查找的路径如图8-45所示，在本次查找中一共读取了三次，这个读取次数在外存访问中是非常重要的，往往就是它反映访问外存设备的速度。

​ 读者也许会疑惑这些查找与外存有什么关系，要知道结点中的关键字（文件名），它自身也带有指针，指向磁盘中的某一个盘块，盘块中记录着文件的大小、位置等相关信息，然后计算机可依据这些信息将外存文件读入到内存。关于外存文件的查找读取读者可阅读微机原理、计算机硬件等相关书籍，在这里只讲解B树用到的数据组织形式的查找原理。

在判断B树的查找效率之前，我们可以先推测一棵深度为H的B树中含有多少个结点：

​ 第1层：1个；

​ 第2层：2个；

​ 第3层：2*⌈m/2⌉个;

​ 第4层：2*⌈m/2⌉2个；

​ ………

​ 第H+1层：2*⌈m/2⌉H-1个；

​ 假设m阶B树的深度为H+1，由于第H+1层为叶子结点，如果当前树中含有N个关键字，则叶子结点必为N+1个，由此可推导出下列结果：

​ N+1 >=2*⌈m/2⌉H-1;

​ H-1<=log⌈m/2⌉ ((N+1)/2);

​ H<= log⌈m/2⌉ ((N+1)/2)+1;

​ 因此在含有N个关键字的B树上进行一次查找，需要访问的结点个数不超过log⌈m/2⌉ ((N+1)/2)+1个。