直接插入排序
直接插入排序(straight insertion sort)把待排序序列视为两部分:一部分为有序序列,通常在排序开始之时将序列中的第一个数据视为一个有序序列;另一部分为待排序序列,有序序列之后的数据视为待排序序列。
如图1中展示的序列arr[],arr[0]~arr[3]视为一个有序序列,arr[4]~arr[9]视为一个待排序序列。
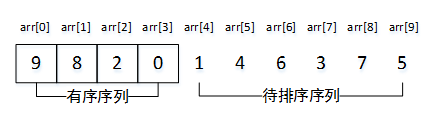
图1 序列arr[]的数据划分
在排序开始之时,从序列头部到尾部逐个选取数据,与有序序列中的数据,按照从尾部到头部的顺序逐个比较(如图2所示),直到找到合适的位置,将数据插入其中。

图2 插入数据选取和比较顺序示意
在比较的过程中,需要一个用来记录待插入数据数值的中间变量,记作tmp;另外为了使叙述清晰,讲述方便,使用一个变量来记录当前比较的数据对应的下标,记作k。以图1中展示的序列为例,此时需要进行的操作,是将待排序序列头部的数据arr[4]=1插入有序序列中。具体操作步骤如下:
(1)用tmp记录元素arr[4],即使tmp=arr[4];以k记录有序序列中当前参与比较的数据对应的下标,即使k=3。
(2)使记录着待插入数据的中间变量tmp与有序序列尾部数据arr[k]进行比较,tmp>arr[k]成立,将arr[k]记录的数据往后移动一个位置,即使arr[4]=arr[k],同时使k=k-1;
(3)使tmp与arr[k]比较。因为tmp>arr[2]不成立,所以比较结束,1应该插入的位置为idx=k+1,将arr[idx]赋为1。
本轮插入排序结束,排序结果如图3所示。
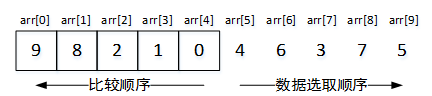
图3 一轮排序结果
下一轮比较中,tmp记录arr[5]的值,k初始化为4,首先使tmp与arr[4]进行比较。
综上所述,假设要对序列arr[n]进行排序,使其按降序有序,序列中有序序列的下标范围为[0,i),无序序列的下标范围为[i,n),执行直接插入排序时,需要进行的基本操作为:
(1)设置中间变量tmp,记录当前无序序列的头部数据,即使tmp=arr[i],记录有序序列尾部数据下标,即使k=i-1;
(2)比较无序序列的表头arr[i]与有序序列的表尾arr[k],
a) 若arr[i]>arr[k],移动arr[k]到下标为i的位置,即使arr[i]=arr[k];同时使k=k-1,使tmp记录的无序表表头数据再次与arr[k]相比较;
b) 若arr[i]<arr[k],说明无序表的表头刚好处于合适位置,此时保持当前序列arr[]不变,使指向待排序序列的指针后移,即使i=i+1。
循环执行步骤(1)(2),直到有序表表头指针指向原序列arr[]的尾部位置或者循环执行n-1遍为止,原序列成为一个降序有序的序列。
下面以int型数组arr[10]= {2, 0, 9, 8, 1, 4, 6, 3, 7, 5}为例,展示使用直接插入排序算法,使arr[10]成为一个降序序列的过程中,每一步排序的结果。如图4所示。

图4 插入排序过程展示
根据以上分析,直接插入排序需要进行多轮比较,在每轮排序中都可能要逐个地移动指针,所以在该算法中也应该使用双层循环。在排序过程中需要使用中间变量来记录过程数据,其中tmp是必须使用的,记录下标的数据k总是与内层循环记录的变量相同或者差1,这里就不再使用。
下面给出使用直接插入排序算法将待排序序列转化为降序序列的代码实现。
//直接插入排序
void InsertSort(int arr[], int n)
{
int i, j;
for (i = 1; i < n; i++)
{
//将数据插入有序表
int tmp = arr[i]; //设置哨兵
if (tmp>arr[i - 1])
{
//将比当前数据大的元素依次后移
for (j = i - 1; j >= 0 && tmp > arr[j]; j--)
arr[j+1] = arr[j];
arr[j+1] = tmp;
}
}
}分析以上代码。代码中使用了双层for循环,第一层循环执行的次数为O(n),所以其时间复杂度为O(n)。在第二层for循环之前有个判断语句,该语句决定第二层循环是否需要执行,最好的情况,是待排序序列刚好是一个降序序列,如此第二轮循环不会执行;最差的情况,是待排序序列是一个升序序列,如此第二轮循环执行的次数为i-1,其时间复杂度为O(n)。所以直接插入排序算法的时间复杂度为O(n2)。
关于该算法的稳定性,因为在判断语句中,使用tmp>arr[i-1]进行判断,明显不会改变两个关键值大小相同的记录在序列中的顺序,所以该算法是一个稳定的算法。
