树形选择排序

树形选择排序（tree selection sort）又称锦标赛排序（tournament sort），是一种按照锦标赛思想进行选择排序的方法。

锦标赛的比赛过程很简单：首先所有参加比赛的选手两两分组，每组产生一个胜利者；其次这些胜利者再两两分组进行比赛，每组产生一个胜利者；之后重复执行上一步骤，直到最后只有一个胜者产生为止。

如图1中为一个按照锦标赛规则进行的比赛，经过三轮比赛，A成为最后的胜利者。

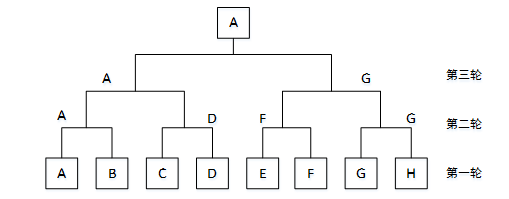
图1 锦标赛比赛过程图

图1中例图结构类似一棵二叉树，以具体比赛成绩代替选手编号，对其表现形式稍作调整，调整后的图如图9-27所示。明显地，图2中的图形是一棵二叉树。

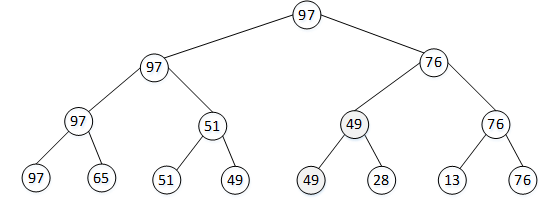
图2 锦标赛的二叉树表现形式

树形选择排序的目的不是选出最值，而是通过这种结构经过选择排序获取一个有序序列。二叉树中叶子结点从左至右可以视为原始序列。以锦标赛比赛规则为基础，使用树形选择排序的过程如下：

（1）首先使树中n个叶子结点代表的记录中的关键字两两分组进行比较，

（2）其次使其中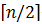个较大者再次两两分组并比较，

（3）如此重复，直到选出当前序列中关键字最大的记录为止。

（4）当一轮比较结束，序列中的最大值会处在根节点的位置。输出并保存根节点，并使其余记录再次重复上述步骤（1）（2）（3）（4）。

以图9-27中的二叉树结构为例，在一轮选择排序之后，找到最大的数据97，将该数据记录并输出。此时对剩下的记录进行一轮树形选择排序，过程中树的构造如图3所示。

图3 树形选择排序第二轮排序图示

第二轮排序时找到次大的数据76，并将其放在根节点，本轮排序结束之后，76被输出，进行第三轮树形选择排序。第三轮排序过程中树的构造如图4所示。

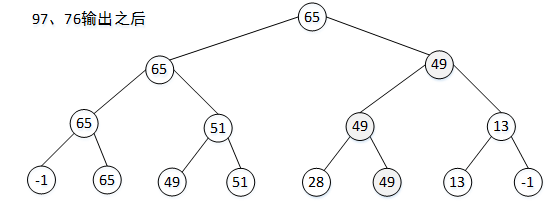
图4 树形选择排序第三轮排序图示

从以上的排序过程可以看出，在排序之前，树形结构的叶子结点依次存放待排序序列的数据。开始排序之后，树形结构中非叶子结点的数值等于左右孩子中较大的一个，如此逐层选择，根节点的数据就是序列中最大的数据。根节点的最大数值输出之后，在叶子结点上使用一个“最小值”来替换该数据（这里使用-1，因为比赛结果都是正值），再次使用锦标的比赛规则两两比较，选出剩余序列中的最大值。如此重复操作，当叶子结点全部成为最小值时，排序结束，此时获得一个降序序列。

由于含有n个子节点的完全二叉树的深度为log2n+1，所以在树形选择排序中，除了最大值（最小值，这里视要获取的序列顺序而定）外，其余数据的选择都需要经过log2n次比较，因此，该算法的时间复杂度为O(nlog2n)。但是这种算法需要借助较多的存储空间，另外即便叶子结点中只剩下一个待排数据，仍要进行多次无用的比较。为了弥补这种算法的缺点，威洛姆斯（J·Willioms）在1964年提出了另一种形式的选择排序——堆排序。