最佳归并树

使用置换-选择排序获得的初始归并段长度可能各不相同。若是归并段的长度不一，对于归并过程中归并段不同的组合方式，内外存之间的读/写次数也不相同。

假设当前由置换-选择排序获得的9个初始归并段的长度分别为：1,14,37,2,6,15,39,8,23，以3-路归并为例，基础的一种归并策略如图1的三叉树所示。

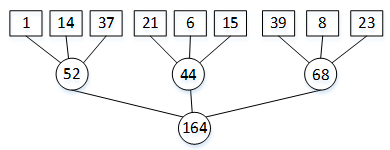
图1 三次归并树

图1中的三叉树又叫3次归并树，表示3-路归并时的归并策略。

在归并树中，叶子结点（又称外结点）表示参加归并的初始归并段，叶子结点到根节点的路径长度表示该归并段在归并过程中参与读/写的次数，非叶子结点（又称内结点）表示其子结点归并生成的新归并段，根结点表示最终的归并结果。对于一棵k次归并树，树中只有度为0的叶子结点和度为k的非叶子结点。

以每个初始归并段的长度为权值，那么归并树的带权路径长度WPL即为归并过程中总的读写次数。对于图1中的三次归并树，它的带权路径长度为：

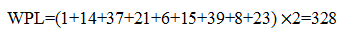
也就是说，使用图1中的归并策略时，归并这9个初始归并段需要在内外存之间读/写各328次。显然使用不同的归并策略，总的读/写次数也不相同。为了提高效率，应该尽量减少读/写次数，那么该如何构造归并树，才能减少读/写次数呢？

在本书前面章节的树中已经学习过霍夫曼树，霍夫曼树是一棵使n个叶子结点带权路径长度最短的二叉树。将霍夫曼树的基本思想应用到k次归并树中：使权值较小的结点远离根节点，即长度较短的初始归并段应尽早归并；使权值较大的结点靠近根结点，即长度越长的初始归并段越晚归并，如此就可以创建最佳的归并策略。

对于图1中的归并树，利用霍夫曼树基本思想加以调整，可以得到图2中的归并树，这棵归并树是所有树中带权路径长度最短的归并树，其WPL=(1+6+8) 3+(14+15+21+23+37) 2+39=301，称为最佳归并树。

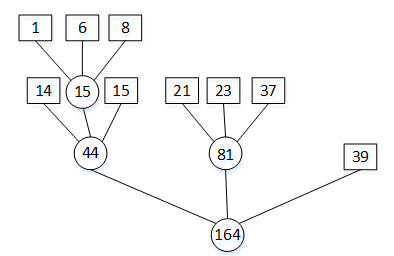
图2 最佳归并树

构建最佳归并树的原理很简单，但是有时候为了构造出一棵真正的k次归并树，可能需要补入一些空的归并段。假设经过置换-选择排序后，共生成了8个初始归并段，其长度分别为：1,14,37,2,

6,15,13,23，那么使用霍夫曼树思想构造3次归并树时，总有一个结点的度只能为2，无法完成归并树的构造。

为了保证归并的读/写次数最少，正确的解决方法是：在初始归并段数目不足以构成k-路归并树时，添加长度为0的“虚段”。按照霍夫曼树构造原则，权值为0的叶子结点离根节点最远，所以长度为0的虚段应该最早参与归并。此时构造的霍夫曼树如图3所示。

图3 8个初始归并段的最佳归并树

那么该如何确定初始归并段的数量是否充足，以及在需要添加虚段时应该添加的虚段的数量呢？分析k叉树，树中只有度为0和度为k的结点，假设度为0的结点的数目为n0，度为k的结点数目为nk，那么nk与n0之间存在这样的换算关系：n0=(k-1)nk+1。变形可得：nk=(n0-1)/(k-1)。也就是说，当(n0-1)/(k-1)=0成立时，这n0个初始归并段刚好可以构成k次归并树，此时内结点有nk个；若(n0-1)/(k-1)=u≠0，那么为了使这u个结点足以构成归并子树，需要添加1个内结点，这个内结点代替一个叶子节点，同时该内结点上有u+1个叶子节点，所以需要添加k-u-1个虚段去构建归并树。

对于图2中的初始归并段，n0=9，k=3，n3=4，满足(n0-1)/(k-1)=0，所以不需要添加虚段；对于图9-63中的的初始归并段，n0=8，k=3，n3=3，(n0-1)/(k-1)=1，所以需要添加3-1-1=1个虚段。