递归函数的应用

递归在C语言开发中并不常用，但有些数学问题，使用递归解决非常简单方便。递归是建立在数学计算的基础上，要求本次计算结果与上一次计算结果相关联，数学中的连加、阶乘等问题，都可以使用递归解决。与循环相比，递归代码更简洁，但却难以理解，而且递归效率要低于循环。

为了增加读者对递归函数地理解与掌握，下面通过一个案例——汉诺塔，更深入的学习递归函数。汉诺塔是一个可以使用递归解决的经典问题，有三根柱子，一根柱子从下往上按照从大到小的顺序摞着64个圆盘，把圆盘从下面开始按照从大到小的顺序重新摆放在另一根柱子上，并规定，在移动过程中，小圆盘上不能放大圆盘，三根柱子之间一次只能移动一个圆盘。问：一共需要移动多少次，才能按照要求移完这些圆盘？三根金刚柱子与圆盘摆放方式如图1所示。

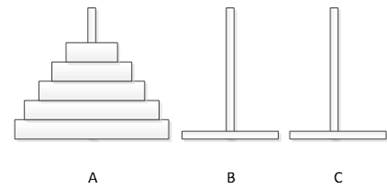
图1 汉诺塔布局图

接下来做一下推算，假设有n个圆盘，移动次数是f(n)：

● 当n = 1时，只需要将圆盘从A座移动到C座，f(1) = 1；

● 当n = 2时，将上面的圆盘移动到B座，A座上第二个圆盘移动到C座，B座上的圆盘再移动到C座，则f(2) = 3；

● 当n = 3时，将A座上第一个圆盘移到到C座，第二个圆盘移动到B座，C座上的圆盘移动到B座，A座上的圆盘移动到C座，B座上的第一个圆盘移动到A座，第二个圆盘移动到C座，A座上的圆盘移动到C座，一共移动了7次，f(3) = 7；

● ......

以此类推，可以得出规律：f(n+1)=2*f(n)+1。

在汉诺塔移动过程中，每一次计算结果都与上一次计算结果有关，可以定义递归函数实现结果计算，如例1所示。

例1 hanoi.c

 1    #define _CRT_SECURE_NO_WARNINGS        //关闭安全检查
 2    #include <stdio.h>
 3    int hanoi(int n)
 4    {
 5        //如果只有一个圆盘，那么只需移动一次即可
 6        if(n == 1)
 7            return 1;
 8        else
 9            return 2*hanoi(n-1)+1;        //当n>=2时，f(n)=2f(n-1)+1
 10    }
 11    int main()
 12    {
 13        int n, num;
 14        printf("请输入汉诺塔的圆盘个数：");
 15        scanf("%d", &n);
 16        num = hanoi(n);
 17        printf("%d个圆盘共需移动 %d 次\n", n, num);
 18        return 0;
 19    }

例1运行结果如图2所示。

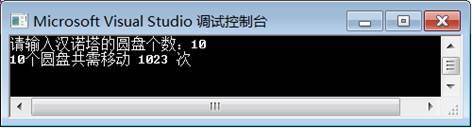
图2 例1运行结果

在例2中，第3~10行代码定义了递归函数hanoi()；第13~15行代码定义了两个变量n和num，并调用scanf()函数从键盘输入一个整数赋值给变量n；第16行代码调用hanoi()函数，将变量n作为参数传递，计算n个圆盘的移动次数，并将结果赋值给变量num。第17行代码调用printf()函数输出num的值。由图7-21可知，当输入10时，10个圆盘的移动次数为1023次。这是一道典型的函数递归调用问题，推算出上下结果之间的规律，利用函数调用本身解决问题。