递归函数的概念 - C语言学习教程_C语言程序_ c语言编程

一种计算过程，如果其中每一步都要用到前一步或前几步的结果，这个计算就是可递归的。用递归过程定义的函数，称为递归函数。在数学运算中，经常会遇到计算多个连续自然数之间的和的情况，例如，要计算1~n之间自然数之和，就需要先计算1加2的结果，用这个结果加3再得到一个结果，用新得到的结果加4…，以此类推，直到用1~(n-1)之间所有数的和加n，就得到了1~n之间的自然数之和。

在程序开发中，要想完成上述功能，除了使用循环，还可以通过函数的递归调用实现，所谓递归调用就是函数内部调用本身的过程。定义计算1~n之间自然数之和的递归函数，示例代码如下：

int getsum(int n)
{
    int sum=0;
    sum = getsum(n - 1);        //调用函数本身
    return sum + n;                //返回sum+n结果，即getsum(n-1)+n结果
}

上述代码定义了getsum()函数，用于计算1~n自然数之和，在函数内部定义了变量sum，并在函数内部调用了函数本身，将求和结果赋值给sum。需要注意的是，getsum()函数的参数为n，在函数内部调用本身时，函数参数为n-1，它表明先计算1~(n-1)之间的自然数之和，最后将（sum+n）的结果返回，这就完成了1~n自然数求和。

定义好getsum()函数之后，在main()函数中调用，系统却抛出“栈溢出”异常，仔细分析程序发现，getsum()函数是一个无止境的函数调用，即没有调用结束条件。例如，传入参数4，计算getsum(4)时，函数会先计算getsum(3)；计算getsum(3)时会先计算getsum(2)…，该过程如图1所示。

图1 getsum(4)无止境递归过程

由图1可知，getsum()函数会从4开始递减，一直递归调用下去，因为函数调用开销较大，很快就会占满栈内存，造成栈溢出导致程序崩溃。程序是求算1~n之间的自然数之和，应当在n递减至1时就停止函数递归调用。如果没有停止条件，递归就是一个内存开销较大的无限循环。由此可以得出，递归函数要满足两个条件：

（1）函数调用本身，且每一次调用本身时，必须是（在某种意义上）更接近于解。

（2）递归必须有结束条件。

通过上述分析，可以修改getsum()函数的定义，添加终止条件，具体如例1所示。

例1 getSum.c

 1    #include <stdio.h>
 2    int getsum(int n)
 3    {
 4        if (n == 1)                        //终止条件：n=1
 5            return 1;                    //n=1时，和为1
 6        int temp = getsum(n - 1);        //调用函数本身
 7        return temp + n;                //返回sum+n结果，即getsum(n-1)+n结果
 8    }
 9    int main()
 10    {
 11        int sum = getsum(4);            //调用递归函数，获得1~4的和
 12         printf("sum = %d\n",sum);        //打印结果
 13        return 0;
 14    }

例1运行结果如图1所示。

图2 例1运行结果

在例1中，第2~9行代码定义了getsum()函数；第11行代码调用getsum()函数计算1~4之间的自然数之和，并赋值给变量sum。第12行代码调用printf()函数输出sum的值。由图7-18可知，调用getsum()函数计算的1~4之间的自然数之和为10。

在本案例中，getsum()函数添加了递归结束条件：n=1，当n从4递减至1时，函数递归结束。下面结合例7-11代码分析getsum(4)的递归调用过程。

（1）n=4，getsum(4)=temp+4=getsum(3)+4。

（2）n=3，getsum(3)=temp+3=getsum(2)+3。

（3）n=2，getsum(2)=temp+2=getsum(1)+2。

（4）n=1，getsum(1)=1，即temp值为1。

递归到n=1时，getsum(1)值为1，将上述过程反推，如下所示。

（1）getsum(2)=getsum(1)+2=1+2=3。

（2）getsum(3)=getsum(2)+3=3+3=6。

（3）getsum(4)=getsum(3)+4=6+4=10。

最终得出1~4之间的自然数之和为10。由于函数的递归调用过程比较复杂，接下来通过一个图例来分析整个调用过程，如图3所示。

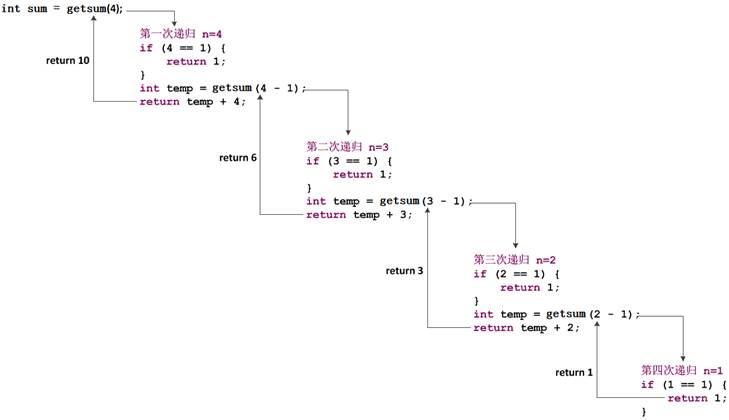
图3 getsum(4)递归调用

图3描述了递归调用的过程，整个递归过程中getsum()函数被调用了4次，每次调用时，n的值都会递减。当n的值为1时，所有递归调用的函数都会以相反的顺序相继结束，所有的返回值会进行累加，最终得到的结果为10。