递归函数

递归是一个函数过程在定义或说明中直接或间接调用自身的一种方法，它通常把一个大型的复杂问题层层转化为一个与原问题相似，但规模较小的问题进行求解。如果一个函数中调用了函数本身，这个函数就是递归函数。递归函数只需少量代码就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

函数递归调用时，需要确定两点：一是递归公式，二是边界条件。递归公式是递归求解过程中的归纳项，用于处理原问题以及与原问题规律相同的子问题；边界条件即终止条件，用于终止递归。

阶乘是可利用递归方式求解的经典问题，定义一个求阶乘的递归函数，代码如下：

def factorial(num):
    if num == 1:
        return 1
    else:
        return num * factorial(num - 1)

利用以上函数求5！，函数的执行过程如图1示。

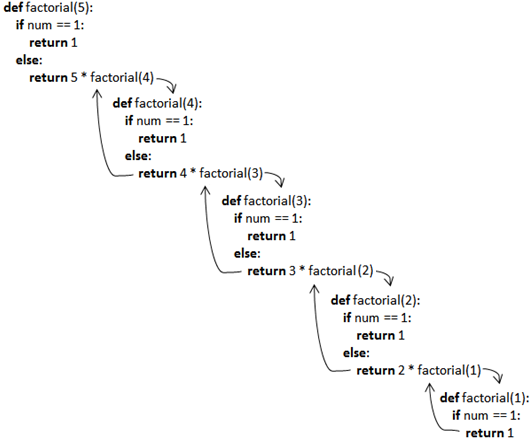
图1 阶乘递归过程

由图1可知，当求5的阶乘时，将此问题分解为求计算5乘以4的阶乘；求4的阶乘问题又分解为求4乘以3的阶乘，以此类推，直至问题分解到求1的阶乘，所得的结果为1，之后便开始将结果1向上一层问题传递，直至解决最初的问题，计算出5的阶乘。