集合关系测试
数学中,两个集合关系的常见操作包括:交集、并集、差集、补集。设A,B是两个集合,集合关系的操作介绍如下:
交集是指属于集合A且属于集合B的元素所组成的集合,
并集是指集合A和集合B的元素合并在一起组成的集合,
差集是指属于集合A但不属于集合B的元素所组成的集合,
补集是指属于集合A和集合B但不同时属于两者的元素所组成的集合。
Python中集合之间支持前面所介绍的四种操作,操作逻辑与数学定义完全相同。Python提供了四种操作符以实现这四项操作,分别是交集(&)、并集(|)、差集(-)、补集(^)。下面以两个圆形表示集合A和B,并使用阴影部分显示四种操作的结果,如图1所示。
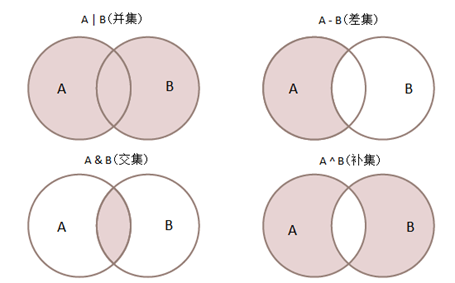
图1 集合间关系的操作
除此之外,Python还提供了4个增强操作符:|=、-=、&=、^=,它们与前面4个操作符的区别是,前者是生成了一个新的集合,而后者是更新了位于操作符左侧的集合。接下来,通过一张表罗列集合S和T之间关系的常见操作,具体如表1所示。
表1 集合间的常见操作
| 常见操作 | 说明 |
|---|---|
| S|T S.union(T) | 返回一个新集合,该集合包含属于S和T的所有元素 |
| S-T S.difference(T) | 返回一个新集合,该集合包含属于集合S但不属于集合T的元素 |
| S&T S.intersection(T) | 返回一个新集合,该集合包含同时属于集合S和T的元素 |
| S^T S.symmetric_difference(T) | 返回一个新集合,该集合包含集合S和T中的元素,但不包含同时属于两者的元素 |
| S|=T S.update(T) | 更新集合S,该集合包含集合S和T所有的元素 |
| S-=T S.difference_update(T) | 更新集合S,该集合包含在集合S中但不属于集合T的元素 |
| S&=T S.intersection_update(T) | 更新集合S,该集合包含同时属于集合S和T的元素 |
| S^=T S.symmetric_difference_update(T) | 更新集合S,该集合包含集合S和T中的元素,但不包含同时属于两者的元素 |
假设有集合a={1,11,21,31,17}和集合b={0,11,20,17,30},它们执行取交集、并集、差集、补集的示例如下:
>>> a = {1, 11, 21, 31, 17}
>>> b = {0, 11, 20, 17, 30}
>>> a|b # 取a和b的并集
{0, 1, 11, 17, 20, 21, 30, 31}
>>> a-b # 取a和b的差集
{1, 21, 31}
>>> a&b # 取a和b的交集
{17, 11}
>>> a^b # 取a和b的补集
{0, 1, 20, 21, 30, 31}对于两个集合A与B,如果集合A中的所有元素都是集合B的元素,那么集合B包含集合A,也就是说集合A是集合B的子集,集合B是集合A的超集;如果集合A中的所有元素都是集合B中的元素,且集合B中至少有一个元素不属于集合A,那么集合A是集合B的真子集,集合B是集合A的真超集。
Python中使用比较运算符可以用来检查某个集合是否为其它集合的子集或者超集,其中,“<”或者“<=”运算符用于判断真子集和子集,“>”和“>=”运算符用于判断的是真超集和超集。需要注意的是,“<”和“>”运算符支持的是严格意义定义的子集和超集,它们不允许两个集合相等;而“<=”和“>=”运算符支持的是非严格意义定义的子集和超集,它们允许两个集合是相等的。例如:
>>> set_one = set('what')
>>> set_two = set('hat')
>>> set_one < set_two # 判断set1是否为set2的严格子集
False
>>> set_one > set_two # 判断set1是否为set2的严格超集
True