线性代数模块
线性代数是数学运算中的一个重要工具,它在图形信号处理、音频信号处理中起非常重要的作用。numpy.linalg模块中有一组标准的矩阵分解运算以及诸如逆和行列式之类的东西。例如,矩阵相乘,如果我们通过“*”对两个数组相乘的话,得到的是一个元素级的积,而不是一个矩阵点积。
NumPy中提供了一个用于矩阵乘法的dot()方法,该方法的用法示例如下。
In [127]: arr_x = np.array([[1, 2, 3], [4, 5, 6]])
In [128]: arr_y = np.array([[1, 2], [3, 4], [5, 6]])
In [129]: arr_x.dot(arr_y) # 等价于np.dot(arr_x, arr_y)
Out[129]:
array([[22, 28],
[49, 64]])矩阵点积的条件是矩阵A的列数等于矩阵B的行数,假设A为 mp的矩阵,B为 pn 的矩阵,那么矩阵A与B的乘积就是一个 m*n 的矩阵C,其中矩阵C的第i行第j列的元素可以表示为:
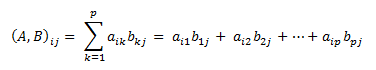
上述矩阵arr_x与arr_y的乘积如图1所示:

图1 矩阵arr_x与arr_y的乘积
除此之外,linalg模块中还提供了其他很多有用的函数,具体如表1所示。
表1 linalg模块的常见函数
| 函数 | 描述 |
|---|---|
| dot | 矩阵乘法 |
| diag | 以一维数组的形式放回方阵的对角线,或将一维数组转为方阵 |
| trace | 计算对角线元素和 |
| det | 计算矩阵的行列式 |
| eig | 计算方阵的特征值和特征向量 |
| inv | 计算方阵的逆 |
| qr | 计算qr分解 |
| svd | 计算奇异值(SVD) |
| solve | 解线性方程组Ax=b,其中A是一个方阵 |
| lstsq | 计算Ax=b的最小二乘解 |
