时序模型—ARIMA

ARIMA模型的全称叫做差分整合移动平均自回归模型，又称作整合移动平均自回归模型（移动也可称作滑动），是一种用于时间序列预测的常见统计模型，记作ARIMA(p,d,q)。

ARIMA模型主要由AR、I与MA模型三个部分组成，有关它们的具体介绍如下：

1. AR模型

自回归模型，表示当前时间点的值等于过去若干个时间点的值的回归——因为不依赖于别的解释变量，只依赖于自己过去的历史值，故称为自回归。如果依赖过于最近的p个历史值，称阶数为p，记为AR(p)模型。

AR(p)模型可以表示为：

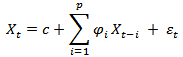
上述公式中，c表示常数项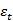，被假设为平均数等于0，标准差等于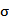的随机误差值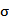，被假设为对于任何的t都不变。整个公式可以用文字叙述为：X的当期值等于一个或数个落后期的线性组合，加上常数项，加上随机误差。

2. I模型

表示的含义是模型对时间序列进行了差分。时间序列分析要求具有平稳性，对于不平稳的序列需要通过一定手段转化为平稳序列，一般采用的手段就是差分。

最简单形式的差分方程如下：

上述公式中，d表示差分的阶数，t时刻的值减去t-1时刻的值，得到新的时间序列称为1阶差分序列。

3. MA模型

移动平均模型，表示的含义是当前时间点的值等于过去若干个时间点的预测误差（预测误差=模型预测值-真实值）的回归。如果序列依赖过去最近的q个历史预测误差值，称阶数为q，记为MA(q)模型。

MA(q)模型可以表示为：

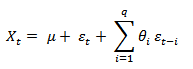
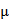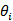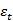其中，是序列的均值，是参数，或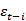都是白噪声。白噪声是一种功率谱密度为常数的随机信号或随机过程，即此信号在各个频段上的功率是一样的。

ARIMA(p,d,q)模型可以表示为：

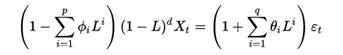
上述公式中共有p、d、q三个参数，它们表示的含义如下：

(1) p--代表预测模型中采用的时序数据本身的滞后数，即自回归项数。

(2) d--代表时序数据需要进行几阶差分化，才是稳定的，即差分的阶数。

(3) q--代表预测模型中采用的预测误差的滞后数，即滑动平均项数。

ARIMA模型的基本思想是：将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列，这个模型一旦被识别后，就可以从时间序列的过去值及现在值来预测未来值。

通常，ARIMA模型建立的基本步骤如下：

(1) 获取被观测的时间序列数据；

(2) 根据时间序列数据进行绘图，观测是否为平稳时间序列。对于非平稳时间序列，需要进行d阶差分运算，转化为平稳时间序列。

(3) 对以上平稳的时间序列，分别求得其自相关系数ACF 和偏自相关系数PACF，通过对自相关图和偏自相关图的分析，得到最佳的阶层p和阶数q。

(4) 根据上述计算的d、q、p得到ARIMA模型，然后对模型进行检验。

需要注意的是，对于一个时间序列来说，如果它的均值没有系统的变化（无趋势），方差没有系统变化，并且严格消除了周期性的变化，就称为是平稳的。