异常值的处理

异常值是指样本中的个别值，其数值明显偏离它所属样本的其余观测值，这些数值是不合理的或错误的。要想确认一组数据中是否有异常值，则常用的检测方法有3σ原则（拉依达准则）和箱形图，其中， 3σ原则是基于正态分布的数据检测，而箱形图没有什么严格的要求，可以检测任意一组数据，下面对这两种检测方法进行一一介绍。

1. 基于3σ原则检测异常值

3σ原则，又称为拉依达原则，它是指假设一组检测数据只含有随机误差，对其进行计算处理得到标准偏差，按一定概率确定一个区间，凡是超过这个区间的误差都是粗大误差，在此误差的范围内的数据应予以剔除。

在正态分布概率公式中，σ表示标准差，μ表示平均数，表示正态分数函数，具体如下：

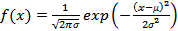
正态分布函数如图1所示。

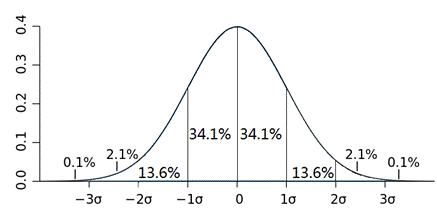
图1 正态分布函数图

根据正态分布函数图可知，3σ原则在各个区间所占的概率如下所示：

（1）数值分布在（μ-σ,μ+σ)中的概率为0.682。

（2）数值分布在（μ-2σ,μ+2σ)中的概率为0.954。

（3）数值分布在（μ-3σ,μ+3σ)中的概率为0.997。

由此可知，数值几乎全部集中在（μ-3σ,μ+3σ)]区间内，超出这个范围的可能性仅占不到0.3%。所以，凡是误差超过这个区间的就属于异常值，应予以剔除。

接下来，自定义一个基于3σ原则的函数，用来检测一组数据中是否存在异常值，具体代码如下。

In [13]: import pandas as pd
         import numpy as np
        # ser1 表示传入DataFrame的某一列
        def three_sigma(ser1): 
            # 求平均值
            mean_value = ser1.mean()
            # 求标准差
            std_value = ser1.std()
            # 位于(μ-3σ,μ+3σ)区间的数据是正常的，不在这个区间的数据为异常的
            # ser1中的数值小于μ-3σ或大于μ+3σ均为异常值
            # 一旦发现有异常值，就标注为True，否则标注为False
              rule = (mean_value - 3 * std_value > ser1) | \
                                                   (ser1.mean() + 3 * ser1.std() < ser1)
            # 返回异常值的位置索引
            index = np.arange(ser1.shape[0])[rule]
            # 获取异常数据
            outrange = ser1.iloc[index]
            return outrange

这里，我们准备了一套符合正态分布的包含异常值的数据，将其保存在example_data.csv文件中。因此，使用 Pandas的read_csv()函数从文件中读取数据，转换为DataFrame对象展示，具体代码如下。

In [14]: # 导入需要使用的包
         import pandas as pd
         file = open(r'E:/数据分析/example_data.csv')
         df = pd.read_csv(file)
         df

Out[14]:
​      A B
   0   1 2
   1   2 3
   2   3 8
   3   4 5
   4   5 6
   5  560 7
   6   2 8
   7   3 9
   8   3 0
   9   4 3
   10  5 4
   11  3 5
   12  2 6
   13  4 7
   14  5 2
   15  23 4
   16  2 5

从输出结果可以看出，位于第5行第A列的数据为560，这个数值比其它值大很多，很有可能是一个异常值。

最后对df对象中的A列数据进行检测，示例代码如下。

In [15]: three_sigma(df['A'])
Out[15]:
5  560
Name: A, dtype: int64

经过3σ原则检测后，返回了索引5对应的数据，也就是刚刚我们看到的异常值。

同样可以检测B列数据中是否存在异常值，示例代码如下。

In [16]: three_sigma(df['B'])
Out[16]: Series([], Name: B, dtype: int64)

从输出结果可以看出，没有返回任何数据，这表明该列数据中不存在异常值。

2. 基于箱形图检测异常值

箱形图是一种用作显示一组数据分散情况的统计图。在箱形图中，异常值通常被定义为小于Q_L – 1.5QR或大于Q_U + 1.5IQR的值。其中：

（1）Q_L称为下四分位数，表示全部观察中四分之一的数据取值比它小；

（2）Q_U称为上四分位数，表示全部观察值中有四分之一的数据取值比它大；

（3）IQR称为四分位数间距，是上四分位数Q_U与下四分位数Q_L之差，其间包含了全部观察值的一半。

离散点表示的是异常值，上界表示除异常值以外数据中最大值；下界表示除异常值以外数据中最小值，如图2所示。

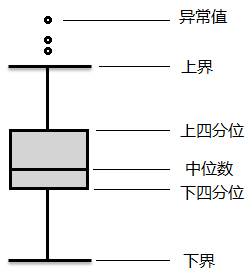
图2 箱形图结构示意图

箱形图是根据实际数据进行绘制，对数据没有任何要求（如3σ原则要求数据服从正态分布或近似正态分布）。箱形图判断异常值的标准是以四分位数和四分位距为基础。

为了能够从箱形图中查看异常值，Pandas中提供了一个boxplot()方法，专门用来绘制箱形图。接下来，根据一组带有异常值的数据绘制箱形图，具体示例代码如下。

In [17]: import pandas as pd
         df = pd.DataFrame({'A': [1, 2, 3, 4],'B': [2, 3, 5, 2],
                            'C': [1, 4, 7, 4],
                            'D': [1, 5, 30, 3]})
        df.boxplot(column=['A', 'B', 'C', 'D'])

Out[17]:
<matplotlib.axes._subplots.AxesSubplot at 0x831b978>

​ 运行效果如图3所示。

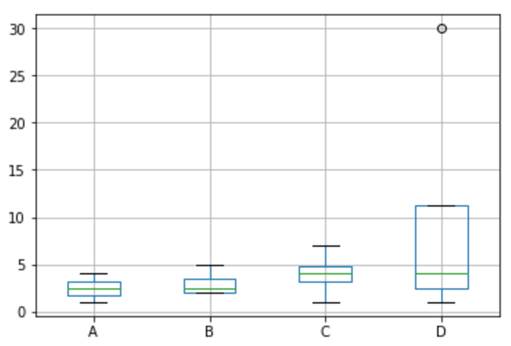
图3 运行结果图

上述示例中，创建的df 对象中共有16个数据，其中有15个数值位于10以内，另一个数值比10大很多。从输出的箱形图中可以看出，D列的数据中有一个离散点，说明箱形图成功检测出了异常值。

检测出异常值后，通常会采用如下四种方式处理这些异常值：

（1）直接将含有异常值的记录删除。

（2）用具体的值来进行替换，可用前后两个观测值的平均值修正该异常值。

（3）不处理，直接在具有异常值的数据集上进行统计分析。

（4）视为缺失值，利用缺失值的处理方法修正该异常值。

异常数据被检测出来之后，需要进一步确认它们是否为真正的异常值，等确认完以后再决定选用哪种方法进行解决。如果希望对异常值进行修改，则可以使用Pandas中replace()方法进行替换，该方法不仅可以对单个数据进行替换，也可以多个数据执行批量替换操作。replace()方法的语法格式如下：

replace(to_replace = None,value = None,inplace = False,limit = None,regex = False,
        method ='pad')

上述方法中部分参数表示的含义如下：

(1) to_replace：表示查找被替换值的方式。

(2) value：用来替换任何匹配to_replace的值，默认值None。。

(3) inplace：接收布尔值，默认为False。

(4) limit：表示前向或后向填充的最大尺寸间隙。

(5) regex：接收boolean或与to_replace相同的类型，默认为False。

(6) method：替换时使用的方法，pad/ffill表示向前填充，bfill表示向后填充。

假设现在有一张菜谱单，它里面列出了菜品的名称以及具体价格，如图4所示。使用箱形图对菜谱中的价格一列进行检测时，发现价格一列中有一个离散点，这个离散点是干锅鸭掌的价格，在询问老板之后得知干锅鸭掌的价格应该为38.8元，只不过在打印的时候漏掉了小数点。

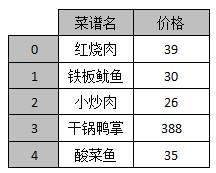
图4 带有异常值的一组数据

接下来，通过一个替换菜单异常价格的示例，演示如何使用replace()方法替换异常值，具体代码如下。

In [18]: import pandas as pd
         df = pd.DataFrame ({'菜谱名': ['红烧肉', '铁板鱿鱼', '小炒肉', '干锅鸭掌', '酸菜鱼'],
                             '价格': [38, 25, 26, 388, 35]})
         df.replace(to_replace=388,value=38.8)

Out[18]:
   菜谱名  价格
0  红烧肉   39.0
1  铁板鱿鱼  30.0
2  小炒肉   26.0
3  干锅鸭掌  38.8
4  酸菜鱼   35.0