顺序存储的原理

上一章简单讲解了线性表的顺序存储结构，读者应对线性表的顺序存储结构原理已有所了解。所谓顺序存储，就是在存储器中分配一段连续的存储空间，逻辑上相邻的数据元素其物理存储地址也是相邻的。假如要用顺序表来存储四个字母，则需要在内存中分配四个连续的存储单元，如图1所示。

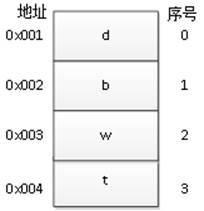
图1 顺序存储结构

在图1中，要存储的四个字母被存储在一段连续的存储空间中。由存储空间的地址可以看出，这四个存储单元是连续的，第一个存储单元由序号0来标记，接下来的存储单元依次递增标记序号，这样在查找元素时，只要找到相应的索引就能找到元素，非常方便。线性表的这种存储方式称为顺序存储或顺序映射，又由于逻辑上相邻的两个元素在对应的顺序表中的存储位置也相邻，因此这种映射也称为直接映射。

在图1中，我们分配了四个存储单元来存储这四个字符，表的长度为4，容量也为4。但要注意的是，表的长度未必与容量相同。表的长度要小于等于表的容量，因为可能申请了四个存储单元，但只存入3个元素。

在顺序存储中，只要确定了线性表在存储空间里的起始位置，线性表中任意元素就都可随机存取，所以线性表的顺序存储结构是一种随机存取的结构。在高级语言中，顺序存储是用数组来实现的。

在顺序存储中，系统不需要为表元素之间的逻辑关系增加额外的存储空间，而且在存取元素时，它可以根据给出的下标快速计算出元素的存储地址，从而达到随机读取的目的。例如在图2-1中，如果要读取第3个元素，因它的下标为2（与第1个元素之间有两个间隔），由内存段的起始地址和元素相差个数可以快速计算出第3个元素的存储地址(0x001 + 1*2 = 0x003)，计算出地址后，就可以方便地对数据进行操作。

但是，如果在顺序表中插入或删除元素，效率会特别低。对插入来说，只限于在表的长度小于表的容量的顺序表中，如果插入大量数据，很难保证空间是否充足。而且一旦分配了存储空间，如果想要扩充容量，需要重新分配空间，然后将原来的数据复制到新的空间中，非常麻烦。另一方面，即使空间充足，那么在插入位置之后的元素必须都要向后移动，这个效率非常低。同理，如果要删除大量元素，那么势必会造成空间的浪费，而且删除元素后，后面的元素都要向前移动，效率也会非常低。