冒泡排序

1、简单的冒泡排序

经过冒泡排序（bubble sort）排列的序列，较大（或较小）的数据会“浮”到序列的顶端（或底部）。冒泡排序的基本原则是：比较两两相邻的记录的关键字，使不满足序列要求的记录交换位置，直到n-1轮循环操作结束。

使用冒泡排序获得降序序列的的基本操作是：

（1）从头部开始，比较相邻的两个元素arr[i]和arr[i+1]，如果第二个元素比第一个元素大，进行数据交换。

（2）指针向后移动，即使i=i+1，再次比较元素arr[i]和arr[i+1]，判断是否需要交换数据。

（3）针对序列中每一对两两相邻的数据重复以上步骤，直到指针指向最后一个位置。

（4）在每一轮循环中重复以上步骤(1)(2)(3)，直到n-1轮循环执行完毕。

至此，得到了一个经冒泡排序有序的序列。冒泡排序和本节开篇讲述的基本排序算法相似：在每一轮排序结束之后都会将待排序序列中的最大值放置在序列的一端；但不同的是：冒泡排序的每一轮指针都在不停移动，做比较的为指针指向的数据和与该数据相邻的数据。而基本排序每一轮的指针固定在一个位置，指针指向的数据逐项与其之后的所有数据比较。

下面以数组int arr[10]= {9, 0, 2, 8, 1, 4, 6, 3, 7, 5 }为例，演示使用冒泡排序获得降序序列的过程。假设在排序过程中指针指向的位置下标为i：

第一轮排序如图9-3所示（图中单箭头指向的为指针的位置，双向箭头指向的两个数据为参与比较的数据）：排序开始时i=0。首先比较arr[0]和arr[1]，因为arr[0]=2，arr[1]=0，arr[0]<arr[1]不成立，所以两个数据位置不变；之后i=i+1，指针指向arr[1]，比较arr[1]和arr[2]，因为arr[1]=0，arr[2]=9，arr[1]<arr[2]，交换两个数据的位置，此时获得序列arr[10]={2,9,0,8,1,4,6,3,7,5}，如图1中①所示。

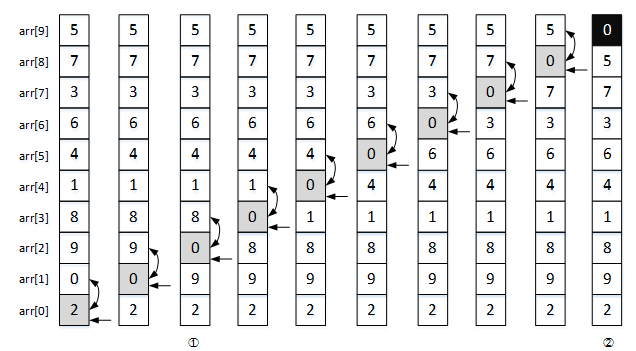
图1 arr[]数组第一轮冒泡排序图示

重复上述步骤，每次比较之后指针后移一位，即i值加1，继续与之相邻数据比较。第一轮经过n-1也就是9次比较之后，得到图1中②所示的结果，在本轮排序中，指针变化范围为arr[0]~arr[8]。可以看出，第一轮冒泡结束后，序列中最小的数据0已经“浮”到了尾部的位置。

之后进行第二轮排序，此时指针重新指向arr[0]，因为第一轮冒泡之后最小的数据已经有序，所以本次不参与比较，第二轮比较的次数为n-2，指针移动的范围为arr[0]~arr[7]。排序过程如图2所示。

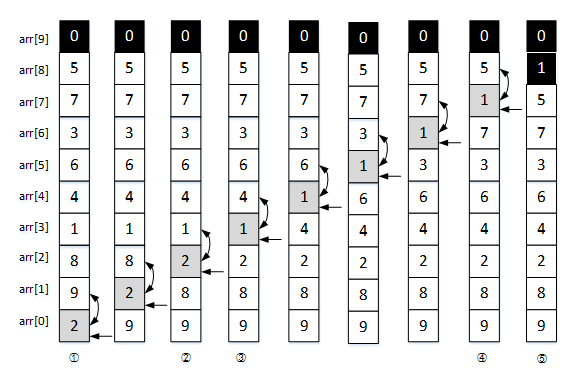
图2 arr[]数组第二轮冒泡排序图示

图2①中指针重新指回arr[0]，再次使arr[0]和arr[1]进行比较。②中参与比较的是arr[2]和arr[3]，因为arr[2]=2，arr[3]=1，arr[2]<arr[3]不成立，所以数据位置不交换，只有指针继续加1移动。③中指针指向arr[3]，记录的数据为1。④中进行第二轮排序的最后一次比较，arr[7]=1，arr[8]=5，arr[7]<arr[8]成立，交换arr[7]和arr[8]。⑤中得到第二轮冒泡排序结果。此时arr[8]和arr[9]已经降序有序。

之后按照一轮、二轮排序规则，继续对剩下的8个数据arr[0]~arr[7]进行排序。在经过7轮排序之后，获得最终的结果。第三到第七轮排序结果展示在图3中，其中带下划线的部分为每轮结果中排列有序的数据。

图3 arr[]数组3~7轮排序结果

根据以上分析，执行冒泡排序时，需要控制每轮指针移动和比较的次数，在这里使用双层循环再自然不过。下面根据冒泡排序的基本原则和操作，给出冒泡排序的算法实现。

//冒泡排序算法实现
void BubbleSort(int arr[],int n)
{
    int i, j;
    for (i = 0; i < n-1; i++)            //从i=0开始，共进行n-1轮排序
    {                                    //每轮排序都使一个较大的值到达较大的位置
        for (j = 0; j < n - i - 1; j++)//每轮两两比较的数据逐层递减
        {
            if (arr[j] < arr[j + 1])
                swap(&arr[j], &arr[j + 1]);    //符合条件则交换
        }
    }
}

分析冒泡排序算法，在该算法中使用了双层for循环，第一层循环的时间复杂度为O(n-1)，第二层for循环的时间复杂度为O(n-i-1)，所以整个算法的时间复杂度为O(n2)。

假设序列中有两个相同的数据，对算法进行分析，其中的判断条件为arr[j]<arr[j+1]，满足此条件时才会发生位置交换，而相等时并不发生位置交换，所以若在排序之前，数据arr[i]在arr[j]之前，排序之后位置相对先后次序仍不变，冒泡排序算法是稳定的。

2、冒泡排序优化

分析图1和2中每轮排序的过程，可以发现，冒泡排序在每轮排序中，除了将最小的数据放在靠后的位置之外，在移动的过程中还使较小一些的数据逐渐靠近合适的位置。比如图2中，数据2本来处于0号位置，而数据2在最终结果中应放置在8号位置，经过2轮排序后，数据2到达了2号位置。在图1中，数据9和8以及其它所有数据与原来相比，也都更靠近其最终需要到达的位置。这也是冒泡排序优于基础交换排序的地方。

分析图3中后面几轮排序的结果，显然在第6轮排序结束之后，就获得了降序有序的序列，但循环还在继续，第6轮之后的排序都是无用功。那么如何避免这些时间的消耗呢？只需在算法中设置一个简单的标志位即可。优化后的算法如下所示。

//冒泡排序算法优化
void BubbleSort_B(int arr[], int n)
{
  int i, j;
  int flag = 1;     //设置标志位
   //需要同时满足i<n-1和标志位不为0才能继续循环
  for (i = 0; i < n - 1&&flag; i++)
  {
​    flag = 0;     //若本轮没有进入if判断语句的执行语句，标志位就为0
​    for (j = 0; j < n - i - 1; j++)
​    {
​      if (arr[j] < arr[j + 1])
​      {
​          flag = 1;          //若本轮进入循环，则修改标志位
​        swap(&arr[j], &arr[j + 1]); //符合条件则交换
​      }
​    }
  }
}

对于前文给出的数组arr[10]，使用该排序算法，明显能降低时间损耗。而在空间上只是多用了一个int型的变量flag，空间复杂度仍为一个常数。

对于优化过的冒泡排序算法，最好的情况，是初始序列已经满足要求的排序顺序，此时时间复杂度为O(n)，最坏的情况，初始序列刚好为要求顺序的逆序，此时时间复杂度为O(n2)，与基础冒泡排序算法时间复杂度相同。另外优化后的冒泡排序不会改变两个键值相同记录的领先关系，仍是一个稳定的算法。