折半查找

折半查找又叫作二分查找，它只能应用于顺序存储的有序序列，其算法思想如下所示：

（1）选择有序表中间位置的记录，比较查找关键字与中间位置元素的关键字，若两者相等，查找成功，否则从中间位置将有序表一分为二。

（2）如果关键字大于中间位置元素，则在后一半有序表中查找，否则在前一半有序表中查找；

（3）重复以上过程，直到找到满足条件的记录。若直到子表不存在，仍未找到要查找的元素，则要查找的元素不存在。

例如有一个包含七个元素的按升序排列int类型数组，如图1所示。

图1 有序数组

在此有序表中查找是值为6的元素，使用折半查找法进行查找的步骤如下所示：

（1）选择有序表中间位置元素4，使它与给定关键字6比较，它与6不相等，则将有序表从中间位置一分为二，如图2所示。

图8-2 取中间位置元素

（2）给定的关键字6大于中间位置的元素4，则在后一半序列表中查找；

（3）在后一半序列表中，取中间位置元素6，与6作比较，如图3所示。

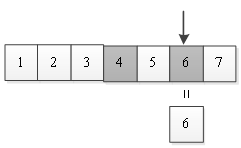
图3 取后半部分有序表的中间部分

（4）其值与给定的关键字6相等，查找成功。

上述即为以图1中的序列为例的折半查找过程。在此次查找中，查找关键字为6的元素只查找了两次，而如果用顺序查找法，需要查找6次。折半查找的优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表必须为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

​ 学习了折半查找的算法过程，那么实现也比较简单了，其代码实现如下所示：

//函数参数：数组、给定的值、有序表的起始位置
int BiSearch(int arr[], const int num, int begin, int last) 
{
    int mid;//中间位置  
    if (begin > last)                 //如果起始角标大于最后一个位置的角标，则错误
    {
        return -1;
    }
    while (begin <= last)
    {
        mid = (begin + last) / 2; //取中间位置
        if (num == arr[mid])
        {
            return mid;             //找到了就将元素对应角标返回
        }
        else if (arr[mid] < num) //如果中间位置的元素小于给定的值
        {
            begin = mid + 1;     //则beg移动到后半部分开头
        }
        else if (arr[mid] > num) //如果中间位置元素大于给定值
        {
            last = mid - 1;      //则last移到前半部分列表的末尾
        }
    }
    return -1;                     //如果没找到，则返回-1
}

除此之外，还可以用递归来实现该算法，因为无论在前半部分有序列表还是在后半部分有序列表，都是重复取中间位置的元素来作比较，所以可递归调用函数。该算法的递归实现如下所示：

int IterBiSearch(int arr[], const int num, int begin, int last)
{
    int mid = -1;
    mid = (begin + last) / 2;
    if (num == arr[mid])
    {
        return mid;
    }
    else if (num < arr[mid])
    {
        return IterBiSearch(arr, num, begin, mid - 1);
    }
    else if (num > arr[mid])
    {
        return IterBiSearch(arr, num, mid + 1, last);
    }
    return -1;
}

对于折半查找来说，如果其消耗的时间复杂度为T(n)：

当n=1时，T(n)=C1;

当n>1时，T(n)= T(n/2)+C2；

其中n/2需要取整数，且C1、C2都是常数。

对于正整数n，有如下推导式：

T(n)= T(n/2)+C2= T(n/4)+2C2= T(n/8)+4C2=……= T(n/2k)+k*C2。

一直推导下去，直到n/2k等于1，也就是k = log2n，此时等式变为T(n)=T(1)+k*C2=C1+ log2n *C2，去除常数项，于是时间复杂度为log2n。折半查找的算法复杂度为O(log2n)，比顺序查找的效率O(n)要高很多。