二叉树的线索化
将二叉树变为线索二叉树的过程称为线索化。按某种次序将二叉树线索化的实质是:按该次序遍历二叉树,在遍历过程中用线索取代空指针。按照遍历方式,线索化也可分为先序线索化、中序线索化和后序线索化。其中先序线索化与后序线索化要比中序线索化稍难,而且在实际开发中也不如中序线索化常用,因此本节以中序线索化为例来学习线索化。
线索化的实质就是使二叉链表结点中的空指针指向该结点的前驱或后继,由于前驱和后继的信息只有在遍历该二叉树时才能得到,所以线索化就是在遍历的过程中修改空指针。
线索化与遍历的算法类似,只需要将遍历算法中访问结点的操作具体化为建立正在访问的结点与其非空中序前趋结点间的线索即可。在该算法中应当附设一个指针pre始终指向刚刚访问过的结点(pre的初值应为NULL),再设置指针p指向当前正在访问的结点,结点pre是结点p的前趋,而p是pre的后继。
线索化的过程虽与遍历相似,但理解起来还是有些困难,下面以上一节中的二叉树为例,分析将二叉树中序线索化的过程,具体步骤如下所示:
(1)根据中序遍历原则可知,遍历的起始结点为H,令指针p和pre都指向起始结点H;根据结点中指针的情况设置结点的左右标志。中序遍历的起点必是叶子结点,叶子结点H的lchild与rchild都是NULL,应当利用起来分别指向该结点的前驱与后继结点,因此设置其ltag与rtag都为1,如图1所示。
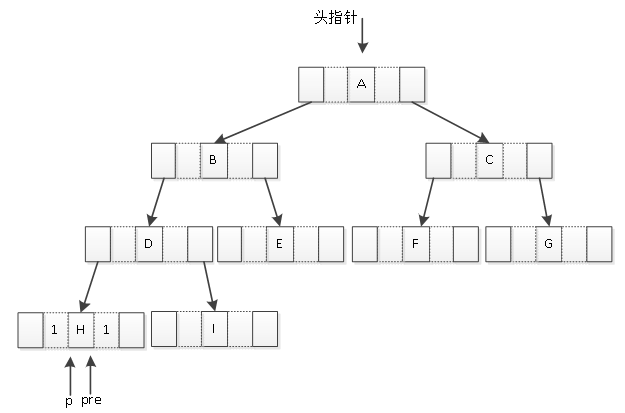
图1 设置起始结点ltag与rtag
(2)H是起始结点,没有前驱,但其rtag值为1,要找寻其后继结点; p指针通过中序遍历查找其后继结点;查找到后继结点为D,则将H结点的rchild指针指向后继结点D;然后设置D结点的ltag与rtag值,如图2所示。

图2 H结点的后继结点D
(3)D结点的ltag与rtag值都为0。将pre移到D结点处,p接着查找中序遍历访问到的下一个结点I,设置I的ltag和rtag值都为1,将I结点的lchild指针指向D,如图3所示。
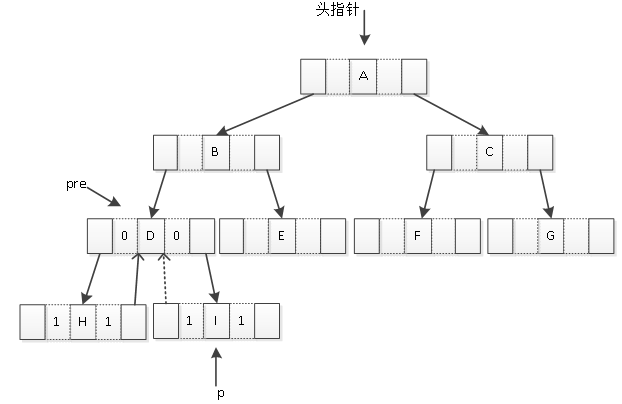
图3 D结点是I结点的前驱
(4)将pre移动到I结点,然后p找到下一个要访问的结点B,设置B结点的ltag和rtag值,都为0;然后令I结点的rchild指针指向后继的结点B,如图4所示。

图4 结点B是结点I的后继
(5)使pre指针指向B结点,p指针找到下一个要处理的结点E,设置E的ltag和rtag值,均为1,将E的lchild指针指向B,即B是E的前驱结点;然后使pre指针指向E结点,p指针查找下一个要处理的结点A,设置A的ltag和rtag值,均为0,则将E的rchild指针指向A,即A是E的后继结点;如图5所示。
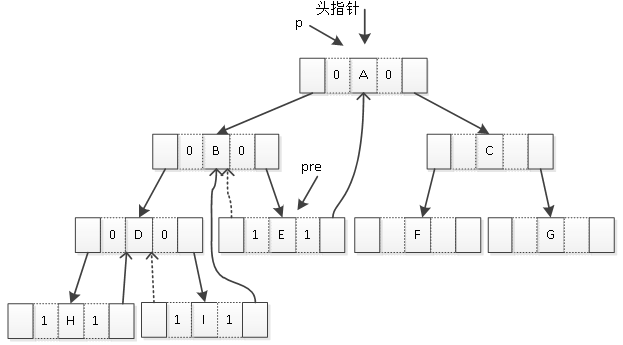
图5 E结点的前驱与后继
(6)使pre指针指向A结点,p指针找到下一个要访问的结点F,设置F的ltag与rtag值,均为1,将F的lchild指针指向A,即F的前驱结点是A;然后使pre指针指向F结点, p指针找到下一个要访问的结点C,设置C的ltag与rtag值,均为0,然后将F的rchlid指向C,即F的后继结点为C,如图6所示。

图6 F的前驱与后继结点
(7)使pre指针指向C结点,p指针找到下一个要处理的结点G,设置G的ltag与rtag值,均为1;然后将G的lchild指向C,即C为G的前驱结点,如图7所示。

图7 G结点的前驱结点为C
最后使pre指针指向最后一个结点处,将p置为空。至此,二叉树的中序线索化完成。理解了线索化的过程,下面给出中序线索化的算法实现,其代码如下所示:
BiThrNode *pre; /* 全局变量,始终指向刚刚访问过的结点 */
/* 中序遍历进行中序线索化 */
void InThreading(BiThrNode *p)
{
if (p)
{
InThreading(p->lchild); // 递归左子树线索化
if (p->lchild == NULL) // 没有左孩子
{
p->LTag = 1; p->lchild = pre; //前驱线索左孩子指针指向前驱
}
if (pre->rchild == NULL) //前驱没有右孩子
{
pre->RTag = 1; pre->rchild = p;//后继线索前驱右孩子指针指向后继(当前结点p)
}
pre = p; //保持pre指向p的前驱
InThreading(p->rchild); //递归右子树线索化
}
}此算法代码与中序递归遍历结构相同,只是在遍历到每一个结点时,需要设置LTag或RTag的值,以及指向结点的前驱或后继的指针。
