基数排序基础

学习基数排序之前，我们先来了解一下计数排序、桶排序和多关键字排序。

1、计数排序

计数排序的基本思想，是当输入的元素是n个[0,k]之间的整数时，设置一个中间数组tmp[n]，使用tmp[data]记录序列中元素data出现的次数；当序列遍历完毕之后，根据tmp[]数组中的计数数据，输出相应次该数据对应的下标。

以数组a[10]= {2, 0, 5, 8, 2, 4, 3, 3, 7, 5 }为例，分析计数排序的排序过程：

（1）遍历一遍该数组，找到其中的最大值，数组a[]的最值为8，根据最大值创建中间变量tmp[8]；

（2）再次遍历数组a[]，记录元素a[i]出现的次数：每当元素a[i]出现时，使tmp[a[i]]计数加1；

（3）第二次遍历结束之后，辅助变量tmp[8]={1,0,2,2,1,1,0,1,1}，其中tmp[2]=2表示元素2在原始序列a[]中出现了2次，tmp[4]=1表示元素4在原始序列a[]中出现了1次，tmp[i]=k表示元素i在原始序列a[]中出现了k次。

（4）根据辅助变量tmp[]中的计数数据，输出tmp[i]次下标i，每输出一次，tmp[i]计数减1，计数数据为0不输出。

最后输出的结果为：0,2,2,3,3,4,5,7,8。

当输入的元素是n个[0,k]之间的整数时，该算法的时间复杂度是O(n+k)。当参与排序的原始序列中元素取值范围较小时，计数排序是一个很高效的线性排序算法，排序的速度快于任何基于比较的排序算法；但是当参与排序的原始序列中元素取值范围很大时，使用计数排序需要占用很大的内存，同时也要耗费很多的时间。

就稳定性而言，计数排序不存在数据比较和交换，是一个稳定的排序。但是这种排序方法，只能排列简单的数字，并且无法输出序列中键值之外的信息。

比如有一个学生表序列，其中的关键字为学生的学号，已知学号的范围为35，对学生表使用计数排序算法，只能排列出学号的顺序，因为无法使用数组的下标存储其它信息，这时若需要输出学号为02的学生对应的其它信息，显然无法完成。

2、桶排序

假设序列包含n条记录，每条记录对应的关键字为k1~kn，首先将这个序列划分成m个子区间，也就是桶，每个桶都是一组n/m的序列，然后根据某种映射关系，对关键字进行判断，将关键字对应的序列映射到第i个桶中，再对每个桶中的所有元素进行比较（可以使用基于交换的任意排序方法），之后依次列举输出这m个桶中的数据，即可得到一个有序序列。

简而言之，桶排序就是根据一定的规则，设置满足各种条件的桶，将待排序的记录分配到其中，使每个桶中的数据有序，再依次输出的一种排序方法。这种方法解决了计数排序中不能为复杂数据排序的问题。

桶排序将一个取值范围较大的、数据元素较多的序列，划分成了多个取值范围较小的、数据元素较少的序列，大大减少了比较的次数。桶排序中的函数映射关系，其作用就相当于快速排序中的划分，将大量数据划分为了基本有序的数据块。

以数组a[10]={13,45,21,67,25,37,58,62,73,51}为例，这些数在区间[0,80]之间，制定7个桶T[1]~T[7]，设定映射规则f(k)=k/10，则第一条记录其关键字为13，根据映射规则f(13)=13/10=1，分配到第1个桶中；第二条记录其关键字为45，根据映射规则f(45)=45/10=4，分配到第4个桶中。当遍历完数组a[]之后，其中的数据分别被分配到划分好的7个桶中。桶中的数据如下：

对每个桶中的数据各自排序，排序之后的数据如下：

最后统一收集这7个桶中的数据，按照桶的编号，将1~7号桶中的数据依次赋值给原始序列，原始序列就成为了一个有序序列。

综合以上分析，对包含n条记录的序列进行桶排序，其核心操作分为两部分：

（1）遍历原始序列，使用映射公式对其关键字进行操作，根据映射结果将记录分配到对应的桶中，这一部分操作的时间复杂度为O(n)；

（2）使用比较排序方法对每个桶中的数据进行排序，这一部分的时间复杂度为 ，其中ni为第i个桶中的数据量。

显然第二部分的操作决定了桶排序的性能优劣。因为基于比较排序的算法最快只能达到O(nlogn)，所以减少每个桶中的数据量是提高效率的唯一办法，而每个桶中的数据量由映射公式和桶的数量决定，所以对于这两个因素，应尽量满足以下两点：

（1）映射公式f(k)能将序列中的n数据尽量平均地分配到m个桶中，这样每个桶就约有n/m个数据；

（2）尽可能地增大桶的数量，对于桶而言，最好的情况是每个桶中只存放一个数据，这样就避免了比较操作。但是桶数量增加，意味着桶集合所需空间增加，空间浪费严重，所以在时间和空间两者之间应有所权衡。

3、多关键字排序

多关键字排序，就是根据一个序列中的多个关键字排序。使用多关键字排序，是因为对于一个序列中的每条记录，没有一个唯一的关键字，可以确定这个记录在序列中的位置。

以生活中常见的场景为例，假设要对一组文件进行排序，但是根据文件类型分类，这些文件可分为A、B、C、D四大类；同时每一种文件内部又有编号，编号从01~10，根据文件的编号进行分类，这些文件又可以分为10组，每一组包含一个编号相同但类型不同的文件（如{A01，B01，C01，D01}）。

假设根据其中的文件类型A、B、C、D进行排序，那么对于每一组编号相同的四个文件，就有44种排序方法，对于整个序列，排序方法更多，如此序列的顺序就难以确定。

但是以文件类型A、B、C、D为主关键字，以文件编号01~10为次关键字，同时根据两个关键字对序列进行排序，就可以得到一个唯一确定的两个关键字都是升序的序列：

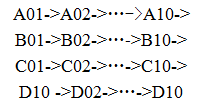
也可以以文件编号01~10为主关键字，以文件类型A、B、C、D为次关键字，同样可以得到一个唯一确定的两个关键字都是升序的序列：

A01->B01->C01->D01->A02->…->D02->…A10->D10

综上，假设有n个记录的序列

{R1，R2，…，Rn}

其中的每条记录Ri对应的m个关键字为(K1,K2,…,Km)，那么对于该序列，所谓的有序是指，对于序列中任意两个记录Ri和Rj（1≤i≤j≤n）都满足下列有序关系：

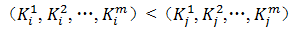
其中K1为最高位关键字，即主关键字；Km为最低位关键字，即最次关键字。对于多关键字排序，通常有两种排序方法：

第一种方法是首先对最高位关键字K1进行排序，将原始序列分成若干个序列，每个序列都有相同的K1值；其次对每个序列按照关键字K2进行分组，使分出的更小的序列包含相同的关键字K2；如此重复，直到对关键字Km-1进行排序之后得到的记录都有相同的关键字（K1，K2，…,Km-1），然后对子序列Km进行排序，最后将所有的子序列依次连接在一起，就得到了一个有序序列。这种方法称为最高位优先（Most Significant Digit first）法，简称MSD法。

第二种方法是首先对最低位关键字Km进行排序，其次对次低关键字Km-1进行排序，如此重复，直到对最高位关键字K1进行排序之后，原始序列成为一个有序序列。这种方法称为最低位优先（Least Signifaicant Gigit first）法，简称LSD法。

MSD和LSD只规定了按照某个关键字的某个顺序（从高到低/从低到高）来进行排序，而不要求对每个关键字进行排序时所用的方法。

根据以上叙述，使用MSD需要不断将序列逐层划分，然后对子序列进行排序，这个过程类似希尔排序中对序列的分组，所以这种方法是一种不稳定的排序方法；使用LSD法进行排序，不必划分子序列，每一次排序都是对完整的序列进行排序，这种方法要求排序过程中使用的排序算法必须是稳定的，即不能改变已排关键字的相对次序。使用这种算法可以不使用前几节中学习的以比较为基础的排序，而是利用分配式排序中的基本思想，通过多次的“分配”和“收集”来实现排序。