B树的插入

在B树中插入元素时，首先要确定此元素在B树中是否存在，如果不存在则在合适位置插入，

否则不能插入，因为B树中不允许有重复值。

在插入时，如果要插入的结点空间足够，即结点中的关键字数量没有达到最大，则可顺利插入；如果要插入的结点空间不足，则将结点进行“分裂”，将一半数量的关键字分裂到新的相邻右结点中，中间关键字则上移到父结点中（如果父结点空间也不足，需要继续“分裂”），同时若结点中关键字向右移动，相关的指针也需要向右移动。

以上一节图1中的B树为例进行讲解。假设向此树中插入元素11，则首先在树中查找是否存在元素11，经查找不存在。那么读取根结点，通过比较发现11小于根结点中的最小元素18，则读取最左边的子结点，如图1所示。

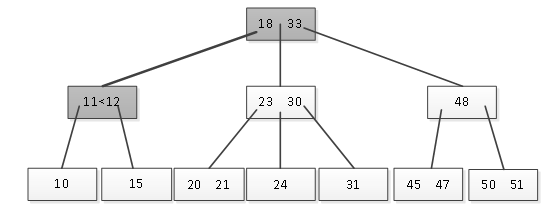
图1 查找插入位置

在子结点中，通过比较发现11<12且结点有足够的空间，则将关键字12向右移动将11插入进来，如图2所示。

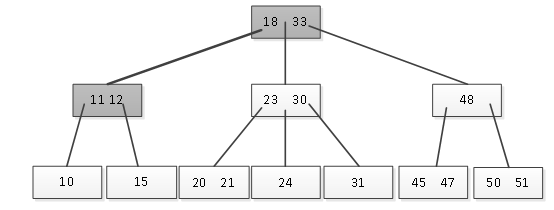
图2 元素11插入成功

在本次插入过程中，一共读取两次，分别是读取根结点、读取子结点；同时所插入位置的结点中写入一次。像这样结点有足够的空间则插入较为简便，但如果要插入的结点空间不足就需要将结点“分裂”。

例如在树中插入元素54，经过查找分析则需要将元素插入到右下解的叶子结点中，如图3所示。

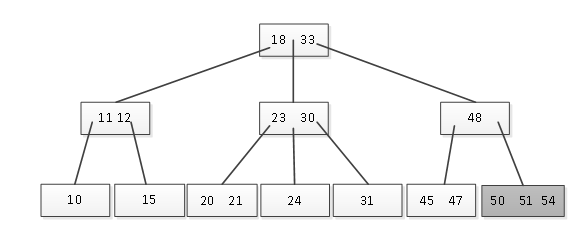
图3 插入元素54

这是一棵3阶树，每个结点只允许有1或2个关键字，显然插入元素54的结点空间不足，那么就需要将结点“分裂”，“分裂”的原则是以中间关键字为界将结点一分为二，产生一个新结点，并把中间关键字插入到父结点中。在此次插入中，三个关键字的排序为50<51<54，则51为中间关键字，将51作为两者的分界上移插入到父结点中，而原来的结点一分为二，将新元素54插入到新分裂出的结点中，如图4所示。

图4 元素54插入成功

这就是B树元素插入的“分裂”过程，这个“分裂”过程可能传达到根结点，此时根结点“分裂”则树会增高一层。在本次插入中，读取次数为三次，写入次数也为三次，底层分裂需要写两次，又将中间关键字写入到父结点中，因此一共写入三次。插入操作如果有“分裂”，最少写入次数就是三次。