从源点到其他顶点的最短路径

假设要从一个地点去往其它多个不同的地点。例如以家为源点，终点可能是学校，可能是商场，可能是公园，以及其它各种地方。将每个地点视为图中的一个顶点，可以这种情况抽象为研究有向网图中从源点到其它顶点最短路径的问题。

解决这类问题，通常使用迪杰斯特拉（Dijkstra）算法。

Dijkstra算法的基本思想是：设G=(V,E)是一个带权有向图，把图中顶点集合V分为两组，一组为已求出最短路径的顶点集S，另一组为未确定最短路径的顶点集合U。初始时S={v}，之后按照最短路径长度的递增次序，每求得一条最短路径(v,…,k)，就将k加入到集合S中，直到全部顶点都加入到S中，算法结束。

下面通过分析具体实例，来学习Dijkstra算法的基本求解思路。以图1中的有向网图G为例。

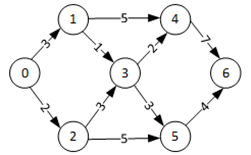
图1 有向网图G

假设给定顶点v0，求解从v0到其余六个顶点v1~v6的最短路径。因为在求解过程中，顶点是逐个遍历的，其最短路径会根据实际情况更新，所以需要设置辅助变量去记录当前找到的从源点v到各个终点的最短路径，设这个辅助变量为dist[]。对辅助变量dist[]初始化：若边(v,vi)存在，则dist[i]为边上权值，否则dist[i]为∞ 。在寻找路径时，若有dist[j]>cvi+wij，则使dist[j]=cvi+wij（cvi 为从源点v到终点i最短路径的长度，wij为弧<i,j>上的权值）。

对算法的基本数据初始化：已求出最短路径的顶点集S={v0}，未确定最短路径的顶点集U={v1,v2,v3,v4,v5,v6}，辅助变量dist[7]={0,3,2, , 。其中dist[0]表示从顶点v0到其自身的路径长度为0，dist[3]~dist[6]表示从源点v0到顶点v3、v4、v5、v6尚无路径，记为 。

然后重复下列操作n-1次，便可找到到达每个顶点的最短路径：

（1）从dist[]数组中找到当前值最小的dist[j]，即dist[j]=Min{dist[i]|i∈E(G)}。

以初始状态为例，只需比较源点与其邻接点之间边上的权值。显然弧<v0,v2>的权值小于弧<v0,v1>的权值，所以选定弧<v0,v2>，此时弧<v0,v2>即为从源点v0到终点v2的最短路径。

（2）将新得的顶点u加入已求出最短路径的顶点集S。

第一遍操作添加v0邻接边<v0,v2>的另一个端点v2。此时S={v0,v2}，U={v1,v3,v4,v5,v6}。

（3）以顶点u为新的中间点，修改顶点v到U中各顶点的距离。

因为通过顶点v2可以访问到顶点v3，其路径长度为dist[2]+w23=5<dist[3]，所以修改dist[]中的dist[3]为5。同样可以访问到v5，dist[2]+w25=7< ，所以修改dist[5]为7。此时dist[7]={0,3,2,5 。

（4）重复步骤（1）（2）（3）。直到集合U为空，或集合S包含所有终点为止。

在dist[]中依次选择源点v到集合U所有顶点中路径长度最小的顶点，比较该顶点已存储的dist[]值和当前获得的最短路径长度加上新出现的弧的权值，选择较小的那个作为dist[i]的值，即使dist[j]=min{dist[j], cvi+wij}。一般对于一个有n个顶点的有向网图，只需执行这些步骤n-1次，便可获取最短路径。

对1中的有向图G使用Dijkstra算法求解最短路径，过程中S、U、dist[]的变化情况与路径选择如下表1所示。

表1 Dijkstra算法求解最短路径

通过上表中表述的步骤，可以发现一个规律：对于一条最短路径，前面步骤中产生的最短路径总是包含在后面产生的最短路径中，即较长的最短路径必定包含次长的最短路径。例如对于⑤中产生的从v0到v4的路径，该路径经过顶点v3，已知v0到v3的最短路径为v0->v1->v3（步骤④），那么v0到v4（较长路径）的最短路径必然包含v0到v3的整个最短路径。

表1中只给出了两条最长路径，其余路径涵盖在这两条路径中。经过6次重复操作，获取顶点v0到其余6个顶点（v1~v6）的最短距离分别为：3，2，4，6，7，11。

结合以上讲解，下面给出Dijkstra算法求解最短路径的算法。

//输出从顶点v出发的所有最短路径
void Dispath(MGraph *G, int dist[], int path[], int S[], int v)
{
    int i, j, k;
    int apath[MAX_VERTEX_NUM], d;    //存放一条最短路径（逆向存放）及其顶点个数
    for (i = 0; i < G->n; i++)        //循环输出从顶点v到顶点i的路径
    {
        if (S[i] == 1 && i != v)
        {
            printf("顶点%d到顶点%d的路径长度：%d\t路径:", v, i, dist[i]);
            d = 0;
            apath[d] = i;                    //添加路径上的终点
            k = path[i];
            if (k == -1)                    //不存在路径
                printf("无路径\n");
            else                            //存在路径
            {
                while (k != v)                //输出路径
                {
                    d++;
                    apath[d] = k;
                    k = path[k];
                }
                d++;
                apath[d] = v;                //添加路径上的起点
                printf("%d", apath[d]);        //先输出起点
                for (j = d - 1; j >= 0; j--)
                    printf(",%d", apath[j]);
                printf("\n");
            }
        }
    }
}
//Dijkstra算法求解最短路径
void Dijkstra(MGraph *G, int v)
{
    int dist[MAX_VERTEX_NUM], path[MAX_VERTEX_NUM];
    int S[MAX_VERTEX_NUM];
    int mindis, i, j, u;
    for (i = 0; i < G->n; i++)
    {
        dist[i] = G->edges[v][i];        //初始化路径长度数组dist[]
        S[i] = 0;                        //S[]置空
        if (G->edges[v][i] < INF)        //路径初始化
            path[i] = v;                //顶点v到顶点i有边时
//置顶点i的前一个顶点为v
        else
            path[i] = -1;
    }
    S[v] = 1;                            //源点v的编号放入S中
    path[v] = 0;
    for (i = 0; i < G->n; i++)            //循环直到所有顶点的最短路径都求出
    {
        mindis = INF;                    //mindis设置初值
        for (j = 0; j < G->n; j++)
        if (S[j] == 0 && dist[j] < mindis)
        {
            u = j;
            mindis = dist[j];
        }
        S[u] = 1;                        //顶点u加入S中
        for (j = 0; j < G->n; j++)
        {
            if (S[j] == 0)
            {
                if (G->edges[u][j] < INF&&dist[u] + G->edges[u][j] < dist[j])
                {
                    dist[j] = dist[u] + G->edges[u][j];
                    path[j] = u;
                }
            }
        }
    }
    Dispath(G, dist, path, S, v);        //最短路径输出
}

算法分析时使用集合S来存储已求出最短路径的顶点，算法中使用一个状态数组S[]，这个数组类似遍历算法中的visited[]：当终点vi求出最短路径时，将S[i]的值设置为1，表示终点vi已加入集合S。

在Dijkstra算法中调用了Dispath()函数，用于输出最短路径。设置了path[]数组，用于记录路径上每一个顶点的前一个顶点。例如path[2]=0，表示对于顶点v2，它的前一个顶点是v0。初始时，若弧<v，i>存在，则path[i][j]=v，否则，path[i][j]= -1。设置了数组apath[]，逆序存储最短路径。

对于前面小节中的有向网图G，它的path[]中每个顶点的前一个顶点记录如表2所示。

表2 path[]数组

使用path[]数组查找最短路径的原则是：首先获得终点，其次根据path[]数组中的值逐步查找前一个顶点，直到前一个顶点为源点为止。

以顶点v6的最短路径输出为例： path[6]=5，即顶点v6的前一个顶点为v5；按照规律查找path[5]，path[5]=2，即顶点v5的前一个顶点为v2；查找path[2]=0，找到源点，查找结束。

查找过程中将找到的值从终点到起点依次存放到数组apath[]中，如路径v0到v6存储为path[]={v6,

v5,v2,v0}，这样就得到了一条逆序的最短路径，之后再对apath[]数组逆序输出，便可得到所求的最短路径。对于每一条路径都是如此。

分析给出的算法：第一个for循环的时间是O(n)，与之并列的第二个for循环外层循环的时间复杂度是0(n)，内层有两个并列for循环，时间复杂度共为O(2n)，所以第二个for循环的时间复杂度为O(n2)。算法结束之前调用了Dispath()函数，该函数中有一个for循环，嵌套了一个while循环，for循环的时间复杂度为O(n)，而while循环内嵌于for循环的if分支中，且终止条件为：k != v，其时间复杂度定小于O(n)，所以Dispath()函数的时间复杂度定小于O(n2)。又因为Dispath()函数与算法中的两个for循环并列，所以Dijkstra算法的时间复杂度为O(n2)。