二叉树的链式存储 - C语言学习教程_C语言程序_ c语言编程

二叉树的链式存储也是利用链表来实现的，链表中的结点存储树结点中的元素和树节点之间的关系。用链表来存储二叉树有两种常用的方式：二叉链表示法，三叉链表示法。那么什么是二叉链，什么是三叉链，接下来我们就来学习一下。

1、二叉链表示法

使用二叉链表表示树，通常树中的每个结点由三部分组成：数据域和左、右指针域。左、右指针分别指示结点的左、右孩子，其结点结构如图1所示。

图1 二叉链表的结点

结点的数据类型定义如下所示：

typedef struct BitNode
{
  DataType data;           //数据域
  struct BitNode* lchild, *rchild; //左右孩子指针
}BitNode;
typedef struct BitNode* BiTree;

其中，数据域data存储结点的数据信息，lchild与rchild分别存储指向左孩子与右孩子的指针，当孩子结点不存在时，相应指针要指向空（NULL）。利用这样的结点结构构建出的链式二叉树被称为二叉链表。使用二叉链表示法来表示图1中的二叉树，其结构如图2所示。

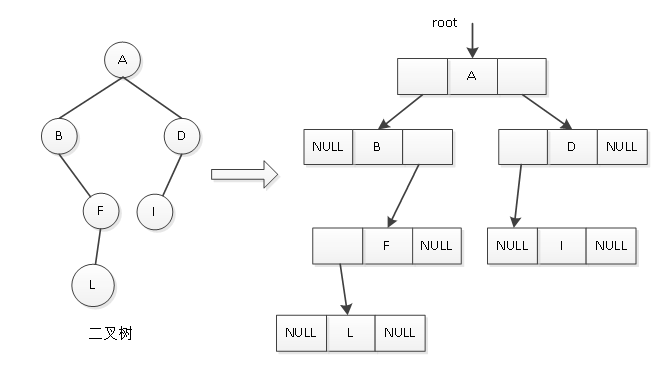
图2 二叉链表示法

一个二叉链表由根指针root唯一确定，若二叉树为空，则root=NULL；若结点的某个孩子不存在，则相应的指针也为空。

具有n个结点的二叉链表中，共有2n个指针域，其中只有n-1个用来指示结点的左、右孩子，其余的n+1个指针域为空。

使用二叉链表存储树时，树的代码实现也比较简单，假如要存储一棵二叉树，树结点中的数据类型为int，则结点定义如下：

typedef struct BitNode
{
  int data;              //数据域，数据类型改为了int
  struct BitNode* lchild, *rchild; //左右孩子指针
}BitNode;
typedef struct BitNode* BiTree;

定义了结点数据类型，就可以定义结点，然后存储结点之间的逻辑关系，代码实现如下所示：

BitNode nodeA, nodeB, nodeC, nodeD, nodeE; //创建5个结点
//将结点都初始化为空，这样可以保证叶子结点相应指针指向空
memset(&nodeA, 0, sizeof(BitNode));
memset(&nodeB, 0, sizeof(BitNode));
memset(&nodeC, 0, sizeof(BitNode));
memset(&nodeD, 0, sizeof(BitNode));
memset(&nodeE, 0, sizeof(BitNode));
nodeA.data = 1; //给结点A赋值
//依次给B、C、D、E结点赋值
nodeA.lchild = &nodeB; //A结点左孩子是B
nodeA.rchild = &nodeC; //A结点的右孩子是C
nodeB.lchild = &nodeD; //B结点的左孩子是D
nodeC.lchild = &nodeE; //C结点的左孩子是E

2、三叉链表示法

使用二叉链表示法虽然可以通过两个指针域便捷地寻找孩子结点，但是无法直接找到当前结点的父结点。为了能够顺利找到结点的父结点，可以以二叉链表中的结点为基础，在结点中添加一个指向父结点的指针parent，形成一个带父指针的结点，使用这种结点构建出的二叉树称为三叉链表。三叉链表的结点结构如图3所示。

图3 三叉链表的结点结构

三叉链表中结点的数据类型定义如下所示：

typedef struct BitNode
{
  DateType data;           //数据域
  struct BitNode* lchild, *rchild; //左右孩子指针
  struct BitNode* parent;      //父指针
}BitNode, *BiTree;

用三叉链表来存储图3中的二叉树，其结构如图4所示。

图4 三叉链表示法

为了便于区别，图4的三叉链表中用细箭头来表示父指针指向。相比于二叉链表的结点结构，它多了一个父指针parent，这种存储结构既便于查找孩子结点又便于查找父结点，但是，它也增加了空间开销。在实际开发中，二叉树存储方法的选择，主要取决于所要实施的各种运算的频度。

多学一招：双亲表示法

二叉树的双亲表示法是另一种存储方法，它利用一维数组来存储树的结点，结点结构中包含结点本身信息，也包含父结点信息，结点结构的数据类型定义如下所示：

typedef struct BPTNode
{
  DataType data; //数据值
  int parentPosition; //存储双亲的位置，数组的下标
  char LRTag; //左右孩子标志域，1表示是左孩子，2表示是右孩子
}BPTNode;

其中data域存储树结点中的数据；parentPosition用来存储双亲的位置；LRTag用来标识自己是左孩子还是右孩子，值为1表示是左孩子，值为2表示是右孩子。

然后定义一个头结点，并记录结点信息、结点数目和根结点，其定义如下所示：

typedef struct BPTree
{
  BPTNode nodes[100];  //存储结点，结点类型是struct BPTNode类型
  int num_node;    //结点数目
  int root;       //根结点的位置，注意此域存储的是父结点在数组中的下标
}BPTree;

有了这两个struct，就可以将一棵二叉树存储起来，它的存储原理是：数组中每一个元素都是一个struct BPTNode类型的结点，它包含三部分信息：结点的数据值，父结点的位置，该是左孩子还是右孩子；这样查找任何一个位置的元素，都可以找出它的父结点以及它和父结点之间的逻辑关系。我们可以用一张图来更清晰直观的表达它的存储原理，如图5所示。

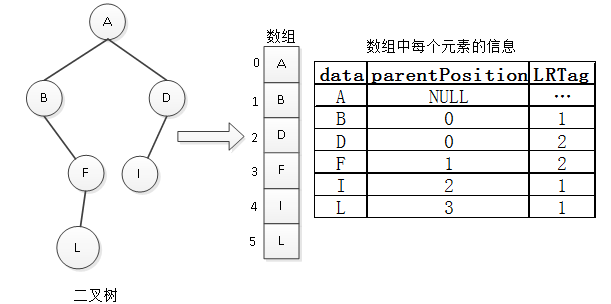
图5 双亲表示法

如图5所示，二叉树的结点存储在数组中，但数组中的每个元素是一个struct BPTNode对象，每个元素的信息如右边的图表所示：

● 0角标位置上元素：data值为A，parentPosition为NULL，说明它没有父结点，是根结点；

● 1角标位置上元素：data值为B，parentPosition=0，说明其父结点在0角标位置，为A；LRTag=1，说明它是父结点的左孩子；

● 2角标位置上元素：data值为D，parentPosition=0，说明其父结点在0角标位置，为A；LRTag=2，说明它是父结点的右孩子；

● 3角标位置上元素：data值为F，parentPosition=1，说明其父结点在1角标位置，为B；LRTag=2，说明它是父结点的右孩子；

● 4角标位置上元素：data值为I，parentPosition=2，说明其父结点在2角标位置，为D；LRTag=1，说明它是父结点的左孩子；

● 5角标位置上元素：data值为L，parentPosition=3，说明其父结点在3角标位置，为F；LRTag=1，说明它是父结点的左孩子。

通过这些信息还原这棵二叉树也很容易。用代码来实现这个存储结构比较简单，下面我们就来实现结点的存储过程，由于篇幅限制，这里只完成A、B、D三个结点的存储，代码如下所示：

BPTree myTree; 
//存储A结点
myTree.root = 0; //数组的0号位置是根结点
myTree.nodes[0].data = 'A';
//存储B结点
myTree.nodes[1].data = 'B';
myTree.nodes[1].parentPosition = 0; //B的父结点是0位置
myTree.nodes[1].LRTag = 1; //B结点是左孩子
//存储D结点
myTree.nodes[2].data = 'D';
myTree.nodes[2].parentPosition = 0; //D的父结点是0位置
myTree.nodes[2].LRTag = 2; //D结点是右孩子

剩余的结点存储与B、D结点相同，只将相应的值更改即可。

使用双亲表示法来存储二叉树是很方便的，在实际项目开发中，如果树不是太复杂，一般都会优先选用此存储方式。