哈希函数的构造方法
哈希函数能使对一个数据序列的访问过程更加迅速有效,通过哈希函数,数据元素将更快被定
位,在构造哈希函数时,要使哈希地址尽可能均匀地分布在散列空间上,同时使计算尽可能简单,冲突次数减少。常用的哈希函数构造方法有以下几种:直接定址法、数字分析法、平方取中法、折叠法、随机数法、除留余数法。接下来我们就来学习一下这几种构造方法。
1、直接定址法
取关键字或关键字的某个线性函数值作为哈希地址,即f(key)=key或f(key)=a*key+b(a,b均为常数),这种哈希函数也叫作自身函数,如果f(key)的哈希地址上已经有值,则往下一个位置查找,直到找到的f(key)的位置没有值,就把元素存放进去。
例如在一场会议中要选拔礼仪,在1500名自愿者中要统计身高165-175cm之间的人数(假设都是整数身高),其中身高作为关键字,哈希值取关键字本身,则哈希表如表1所示。
表1 直接定址法构造哈希函数
| 关键字 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 哈希值 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 人数 | 120 | 90 | 130 | 360 | 220 | 80 | 100 | 96 | 152 | 80 | 52 |
当不同的会场需要不同身高的礼仪时,如7号会场需要170cm身高的礼仪20名,则可快速通过此哈希表来查找170cm身高的人数有多少。
直接定址这种计算方法比较简单,并且不会发生冲突,但当关键字分布不连续时,会出现很多空闲单元,造成大量存储单元的浪费,在实际应用中,这种方法的适应性并不强。
2、数字分析法
数字分析法是取数据元素关键字中某些取值较均匀的数字位作为哈希地址的方法,即当关键字的位数很多时,可以通过对关键字的各位进行分析,丢掉分布不均匀的位,作为哈希值。
例如,传智的员工登记表以员工编号作为关键字,员工编号一共有有9位,例如010110001,前三位表示哪个分校,如010表示北京分校,第四位表示哪个部门,第五位表示在该部门担任的职位,最后四位则表示员工的具体编号,如0100表示公司第100位入职的员工。那么针对这种情况我们可以取员工编号的后四位作为哈希地址,如表2所示。
表2 数字分析法构造哈希函数
| 关键字 | 哈希值 | 员工信息 |
|---|---|---|
| …… | …… | ……. |
| 010020093 | 0093 | ……. |
| 010020094 | 0094 | ……. |
| 010130095 | 0095 | ……. |
| 010250096 | 0096 | ……. |
| …… | ……. | …… |
在此哈希表中,取关键字的后四位作为哈希地址,在查找某一编号的员工信息时,就可以直接跳到后四位数字所标识的地址空间,查找起来比较高效。
数字分析法比较简单、直观,但通常适用于关键字已知且关键字的位数比较大的情况,这就限制了它的使用范围。
3、平方取中法
这是一种比较常用的哈希函数构造方法,这个方法是先取关键字的平方,然后再根据可使用空间的大小,选取平方数的中间几位作为哈希地址。它的原理是通过取平方扩大差别,平方值的中间几位和这个数的每一位都相关,则对不同的关键字得到的哈希函数值不易产生冲突,由此产生的哈希地址也较为均匀,取的位数由表长决定。
假设哈希表长为1000,则可取关键字平方的中间三位,如表3所示。
表3 平方取中法构造哈希函数
| 关键字 | 关键字的平方 | 哈希函数值 |
|---|---|---|
| 1234 | 1522756 | 227 |
| 2143 | 4592449 | 924 |
| 4132 | 17073424 | 734 |
| 3214 | 10329796 | 297 |
平方取中法是最接近于“随机化”的构造方法,它一般适用于不了解关键字分布而关键字位数又不是很多的情况。
4、折叠法
所谓折叠法是将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几位的叠加和(舍去进位)作为哈希地址。这种方法适用于关键字位数较多,而且关键字中每一位上数字分布大致均匀的情况。
折叠法中数位折叠又分为两种:移位叠加和边界叠加;移位叠加是将分割后每一部分的最低位对齐,然后相加;边界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。
例如,当哈希步长为1000时,关键字key=110108331119891,允许的地址空间为三位十进制数,则这两种叠加情况如图1所示。
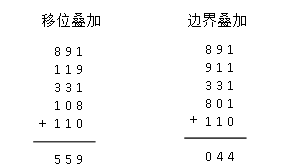
图1 折叠法求哈希地址
用移位叠加求得的哈希地址是559,而用边界叠加所得到的哈希地址是44,如果关键字不是数
值而是字符串,则可先利用ASCII码将其转化为数值。折叠法不需要事先知道关键字的分布,适合关键字位数较多的情况。
5、除留余数法
假设哈希表的表长为m,则某一个小于等于m的数p作为关键字的除数,所得的余数作为哈希地址,即f(key)=key%p(p<=m),除数p称为模,这是一种最简单也最常用的哈希函数构造方法。
除留余数法不仅可以对关键字直接取模,也可以在折叠、平方取中等运算后取模。在使用除留余数法时,模p的选择很重要,如果选值不当,容易产生同义词。例如,若p含有质因子x,则所有含x因子的关键字其哈希地址均为x的倍数。一般情况下,p值可以为质数,或者不包含20以下质因数的合数。理论研究表明,除留余数法的模p取不大于表长且最接近表长m的素数为最好。
6、随机数法
随机数法就是用随机函数获取一个随机值作为哈希地址,即f(key)=random(key),random()是产生随机数的函数。当关键字长度不等时可以采用此方法来构造哈希函数。
实际应用时,需要根据不同的情况采用不同的哈希函数。主要考虑的因素有:计算哈希函数所需要的时间、关键字的长度、哈希表的大小、关键字的分布情况、记录查找频率等。此外,构造哈希函数时必须尽量减少冲突的情况,由于实际应用的复杂多样性,冲突往往不可避免。因此在构造哈希函数时除了要考虑以上的几个因素外,还要尽量做到让关键字的地址均匀分布在哈希表中,以减少冲突现象。其次要尽量选择计算简单的哈希函数,以提高地址的计算速度。总之,一个好的哈希函数应当均匀以减少冲突,简单以提高计算速度。
