堆排序
1、堆
在学习堆排序之前,我们先来了解一下堆。本节用到的堆为二叉堆,是一种特殊的完全二叉树。堆的定义如下:一个含有n条记录的序列,当且仅当满足以下关系时,称之为堆。
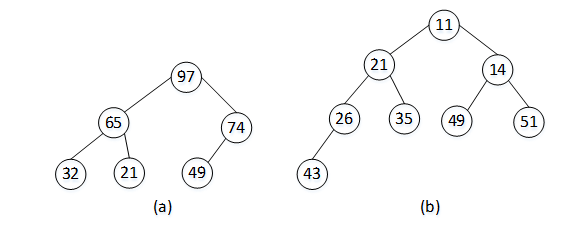
图1 二叉堆举例
使用一维数组存储,图9-30中的堆分别表示如下:
(a) 大顶堆:{97,65,74,32,21,49};
(b) 小顶堆:{11,21,14,26,35,49,51,43}。
2、如何实现堆排序
使用堆排序(heap sort)只需要额外的一个序列大小的辅助空间,每条待排序记录仅占一个存储空间。当堆调整为大顶堆(或小顶堆)之后,输出堆顶元素,使剩余的n-1个元素组成的待排序序列再调整为大顶堆(或小顶堆)。如此便能得到一个降序序列(升序序列),这个排序过程称为堆排序。
待排序序列可以简单地使用一维数组存储,但初始的序列并不满足堆的定义;排序过程中输出堆顶之后,剩余的序列同样需要稍作调整,才能成为一个堆。综上,堆排序有两个关键问题:一是如何调整一个无序序列,使其成为一个堆;二是如何在堆顶输出之后,调整剩余的序列,使其成为一个堆。
首先探讨第二个关键问题。
当堆顶输出之后,剩余的序列构成了原堆顶的左右子树,当前序列的堆顶应在这两棵子树中产生。根据堆的定义可知,此时的两棵子树皆为一个堆,所以新的堆顶元素会在原序列的左右孩子之间产生。
用最后一个元素代替堆顶元素,通过使之不断地与其左右孩子比较,调整该序列重新构成一个堆。以图2 (a)中的大顶堆为例,其调整过程如图2所示。
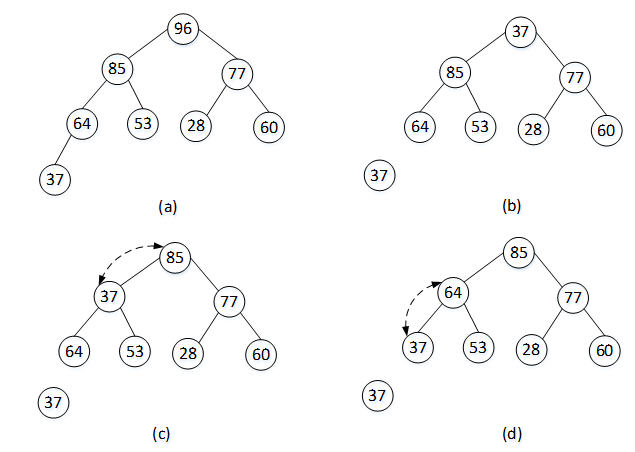
图2 大顶堆排序过程示意图
对于图2(a)中的大顶堆,当堆顶元素96被输出之后,将序列末尾元素37放在堆顶位置,并使其左右孩子比较(图2(b));比较发现左孩子85大于右孩子77,使堆顶元素37与其左孩子85比较,37<85,交换37与85(图2(c));继续为元素37寻找合适的位置,此时其左右孩子分别为64和53,比较左右孩子,左孩子64较大,37<64,使其与左孩子进行交换(图2(d))。到此37已经是叶子结点,此时序列调整完毕,成为一个新的大顶堆,堆顶元素85为继96之后的最大值。
对以上步骤进行总结:
(1)在堆顶被输出之后,将剩余序列的末尾元素data[i]放在堆顶位置;
(2)选取该元素左右孩子中较大的一个nChild与之比较,若data[i]>nChild,使data[i]与nChild进行交换;否则表示该元素已找到合适的位置,终止循环;
(3)重复步骤(3),直到该元素成为叶子结点为止。
在之后的排序中,每当序列被调整为一个大顶堆,并且堆顶元素被输出,就执行上述步骤(1)~(3),直到该步骤执行n-1遍为止。
至此第二个关键问题已经分析完毕。上述操作是从一个大顶堆开始的,所以我们还需要分析第一个关键问题:如何调整一个无序序列,使其成为一个堆。此处以将无序序列调整为大顶堆为例。
假设有一个无序序列arr[8]={28,64,60,85,53,77,96,37},其构成的完全二叉树T如图3所示。
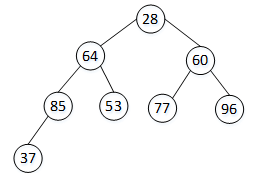
图3 arr[]的二叉树表现形式
当前的二叉树T为一个无序的完全二叉树,根据堆的定义,每个非终端结点中存储的数据需要大于其左、右孩子结点中存储的数据,所以从最后一个非终端的结点开始操作,使其与左、右孩子结点存储的数据比较,并进行调整。
使用i表示结点的下标,根据完全二叉树的定义,最后一个非终端结点在一维数组中的下标为i=(n-1)/2,图3中的二叉树共有8个结点,则最后一个非终端结点为arr[3];结点左右孩子的下标分别为lChild=i*2+1,rChild=lChild+1,所以arr[3]的左、右孩子分别为arr[7]和arr[8];因为n=8,所以结点的下标范围应为0~7,也就是说arr[3]不存在右孩子。
使arr[3]与其左孩子arr[7]比较,arr[3]>arr[7],所以结点的顺序不发生改变。当前序列如图4所示。

图4 对结点arr[3]操作后的结果
排在当前非终端结点前的非终端结点,其下标为i=i-1,也就是arr[2];arr[2]的左、右孩子分别为arr[5]和arr[6],首先比较arr[5]与arr[6],其中较大的数据为arr[6];再使arr[2]与arr[6]比较,因为arr[2]<arr[6],所以交换arr[2]和arr[6]。交换后的二叉树如图5所示。
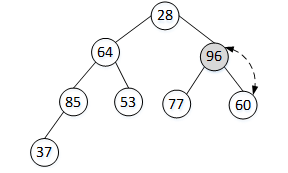
图5 对结点arr[2]操作后的结果
重复之前的步骤,使i=i-1,i=1,对结点arr[1]进行比较操作,arr[1]小于其较大的孩子arr[3],交换arr[1]和arr[3],此时的arr[3]是非终端结点,所以需要对其左、右孩子进行判断,若arr[3]小于其左右孩子,则与较大的孩子结点进行交换。本轮排序的结果如图6所示。
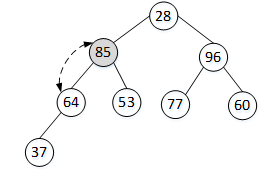
图6 对结点arr[3]操作后的结果
排在当前非终端结点前的非终端结点,其下标为i=i-1,也就是arr[2];arr[2]的左、右孩子分别为arr[5]和arr[6],首先比较arr[5]与arr[6],其中较大的数据为arr[6];再使arr[2]与arr[6]比较,因为arr[2]<arr[6],所以交换arr[2]和arr[6]。交换后的二叉树如图7所示。
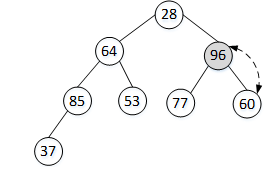
图7 对结点arr[2]操作后的结果
重复之前的步骤,使i=i-1,i=1,对结点arr[1]进行比较操作,arr[1]小于其较大的孩子arr[3],交换arr[1]和arr[3],此时的arr[3]是非终端结点,所以需要对其左、右孩子进行判断,若arr[3]小于其左右孩子,则与较大的孩子结点进行交换。本轮排序的结果如图8所示。

图8 对结点arr[1]操作后的结果
继续重复之前的操作,使i=i-1,i=0,本轮操作为最后一次操作。arr[0]的左孩子arr[1]小于其右孩子arr[2],比较arr[0]与arr[2],arr[0]<arr[2],交换arr[0]和arr[2]。此时操作的结果如图9(a)所示。
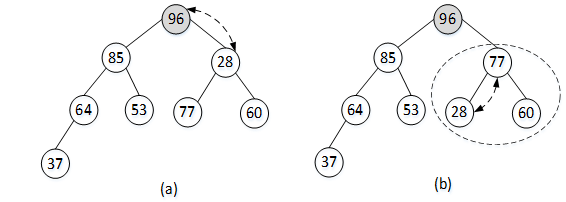
图9 对结点arr[0]进行的操作
可以看出此时arr[2]小于其左、右孩子结点,所以对arr[0]的子树,仍要重复执行上述操作。最终的排序结果如图10所示。

图10 大顶堆创建结果
经过上述步骤,无序序列arr[]被调整为一个大顶堆。
分析以上步骤发现,将一个无序序列调整为一个堆的过程,就是对完全二叉树中每个非叶子结点执行关键问题二中三个步骤的过程。也就是说,对无序序列中的每个非叶子结点执行一遍关键问题二中的操作,这个无序序列就会成为一个堆。
3、堆排序的算法实现
下面给出堆排序的算法实现。
//调整算法
void HeapAdjust(int arr[], int i, int n)
{
int nChild;
int tmp;
for (; 2 * i + 1 < n; i = nChild)
{
//子结点的位置=2*(父结点位置)+1
nChild = 2 * i + 1;
//得到子结点中较大的结点
if (nChild<n - 1 && arr[nChild + 1]>arr[nChild])
++nChild;
//如果较大的子结点大于父结点,那么把较大的子结点往上移动,替换它的父结点
if (arr[i]< arr[nChild])
{
tmp = arr[i];
arr[i] = arr[nChild];
arr[nChild] = tmp;
}
else break; //否则退出循环
}
}
//堆排序算法
void HeapSort(int arr[], int n)
{
int i;
//对序列中的每个非叶子结点执行调整算法,使该序列成为一个堆
for (i = (n - 1)/ 2; i >= 0; i--)
HeapAdjust(arr, i, n);
//从最后一个元素开始对序列进行调整,不断缩小调整的范围直到第一个元素
for (i = n - 1; i > 0; i--)
{
//把第一个元素和当前的最后一个元素交换
//保证当前最后一个位置存放的是现在这个序列中最大的元素
arr[i] = arr[0] ^ arr[i];
arr[0] = arr[0] ^ arr[i];
arr[i] = arr[0] ^ arr[i];
//不断缩小调整heap的范围,每一次调整完毕保证第一个元素是当前序列的最大值
HeapAdjust(arr, 0, i);
}
}算法中的“调整算法”——HeapAdjust()对应关键问题二中的操作步骤,每次执行都是对以一个非叶子结点为根结点的子树进行调整,使这一棵子树成为一个堆。堆排序算法中包含两个for循环:第一个for循环对每一个非叶子结点依次执行调整算法,执行完毕之后,初始的无序序列被调整为一个堆。第二个for循环首先将当前序列中末尾的结点与根节点交换,此时相当于将堆顶保存到后半部分的序列中;其次以处于堆顶的元素为根结点,执行一次调整算法,使剩余待排序序列调整为堆。执行完毕之后,排序算法结束,获得一个有序序列。
从算法分析可以看出,虽然每次调整都找到了最大的元素,但是该元素被放置在末尾位置,所以对一个大顶堆求解,得到的序列是一个升序序列。
分析该算法的时间复杂度。堆排序算法包含构建堆的算法和堆排序的算法两部分,其主体为两个for循环,这两个for循环都用到了调整算法。调整算法的主体是一个for循环,调整的时间复杂度与结点所在深度有关,是一个log2n的操作,时间复杂度为O(log2n)。构建堆的算法从(n-1)/2处开始,一直处理到第一个位置为止,过程中操作时间相当于每个被操作的结点所在的深度之和,即O(h1)+O(h2)+…+O(h(n-1)/2),结果为O(n)。堆排序的算法是利用前面两个步骤完成的,其中构建堆的步骤被调用了一次,调整堆的算法被调用了n-1次,所以堆排序的时间复杂度为O(nlog2n)。
