霍夫曼树的构造

树的带权路径长度越小其运算效率越高，但是如何构造出一棵霍夫曼树呢？根据霍夫曼提出的构造最优二叉树的算法思想，构造霍夫曼树的基本步骤如下所示：

（1）有n棵权值分别为w1、w2、w3、…、wn的二叉树，其左右子树都为空（可理解为是确定权值的结点）；

（2）从中选取出权值最小的两棵树组成一棵新的树。如果有结点权值相同的，可以任选两棵，为了保证新树仍是二叉树，需要增加一个新结点作为新树的根，将所选的两棵树作为新树根的左右子树，不分先后，将两个孩子的权值之和作为新树根的权值。删除已经选中的树，使新生成的树参与下一轮选择。

（3）对新树集重复步骤（2），直到集合中剩下最后一棵二叉树，这棵二叉树便是霍夫曼树。

为了让读者更好的理解霍夫曼树的构造过程，下面我们用图示来分析这个构造过程。

（1）有一片确定权值的二叉树森林，如图1所示。

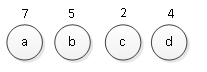
图1 确定权值的森林

（2）从中选出权值最小的两棵二叉树，为c和d，新增加一个根结点，以两个孩子的权值之和作为新的根结点的权值。如图2所示。

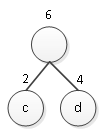
图2 新二叉树

将c和d结点从集合中删除，将新生成的树放入集合中。

（3）然后再从剩下的森林中找出两棵权值最小的树，权值为6与5的两个棵，组成一棵新二叉树，如图3所示。

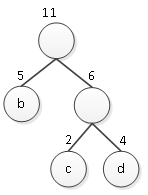
图3 新二叉树

将选中的两棵树从集合中删除，将新生成的二叉树放入集合。

4、再从集合中选出两棵权值最小的树组成一棵新的二叉树，如图4所示。

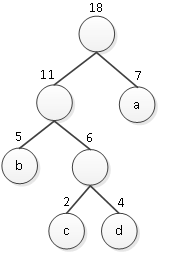
图4 新二叉树

至此，森林中只剩下如图6-76中的这一棵二叉树，这就是一棵霍夫曼树。它的带权路径长度为7×1+4×3+2×3+5×2 = 35。

霍夫曼树的应用非常广，在不同的应用中叶子节点的权值可以作不同的解释。霍夫曼树应用于信息编码中，权值可以看成某个符号出现的频率；应用到排序过程中，权值可以看成是已排好次序，等待合并的序列长度等。

需要注意的是：初始森林中的二叉树都是孤立的结点。n个结点需要合并n-1次，新增n-1个新结点，最终求得的霍夫曼树共有2n-1个结点。霍夫曼树是严格的二叉树，没有度数为1的结点。