拓扑排序
设G=(V,E)是具有n个顶点的有向无环图,对其进行拓扑排序,是将G中所有顶点排成一个线性序列,使得对于图中任意一对顶点u和v,若边(u,v) ∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序的序列,简称拓扑序列。简单地说,在一个有向无环图中找一个拓扑次序的过程,称为拓扑排序。
一个有向图可以用来表示一个流程图,它可以是一个工地施工流程图,一个车辆生产流程图,或者是一个数据流图,图中的每个顶点表示一个活动,每一条有向边表示两个活动之间的次序关系。
举例说明,一个计算机专业的学生,必须学习一系列专业课程,像《C语言》、《高等数学》、《离散数学》、《数据结构》、《编译原理》、《操作系统》、《专业英语》等等。其中《高等数学》是基础课程,没有先修课程,可以随时安排;但学习《数据结构》之前通常先学习《C语言》和《离散数学》。这些条件规定了这些课程之间的次序关系,通常用有向图表示这种关系,图中的顶点表示课程,有向边表示课程修读的先后顺序。
这种用顶点表示活动,用有向边表示活动间优先关系的有向图称为AOV-网(activity on vertex network),即顶点表示活动的网。
假设课程间的关系如表1所示。
表1 课程关系表
| 课程编号 | 课程名称 | 先修课程 |
|---|---|---|
| C1 | C语言 | 无 |
| C2 | 高等数学 | 无 |
| C3 | 离散数学 | C2 |
| C4 | 数据结构 | C1、C3 |
| C5 | 编译原理 | C1、C4 |
| C6 | 操作系统 | C4、C5、C7 |
| C7 | 专业英语 | C4 |
根据表1得出表示课程间关系的有向图G,如图1所示。
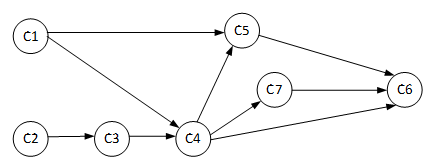
图1 课程关系示意图
对这个课程关系示意图进行拓扑排序,可以得到拓扑序列:C1-C2-C3-C4-C7-C5-C6,也可以得到拓扑序列:C1-C2-C3-C4-C5-C7-C6。拓扑排序的结果并不唯一,还可以得到其它的拓扑序列,只要符合课程间的既定次序,学生可以任意选择一个序列按序学习。
拓扑排序的方法也很简单,其规则如下:
(1)从有向图中选择一个没有前驱(入度为0)的顶点,并将顶点输出;
(2)从图中删除这个顶点,同时删除从该顶点出发的所有边;
(3)重复上述两步,直到图中不再存在没有前驱的顶点为止。
对图7-27中有向图求解拓扑序列的步骤如下:
(1)图中C1和C2都没有前驱,任选C1,删除有向边<C1,C4>,<C1,C5>。
(2)没有前驱的顶点为C2、, 输出C2,删除有向边<C2,C3>。
(3)此时没有前驱的顶点只有C3,输出C3,删除有向边<C3,C4>。
(4)没有前驱的顶点只有C4,输出C4,删除有向边<C4,C5>,<C4,C7>,<C4,C6>。
(5)没有前驱的顶点为C5、C7,任选C7输出,删除有向边<C7,C6>。
(6)此时没有前驱的顶点只有C5,输出C5,删除有向边<C5,C6>。
(7)最后输出顶点C6,顶点输出完毕,得到拓扑序列C1-C2-C3-C4-C7-C5-C6。
求解过程中的图中尚未参与排序的顶点与边如图2所示。
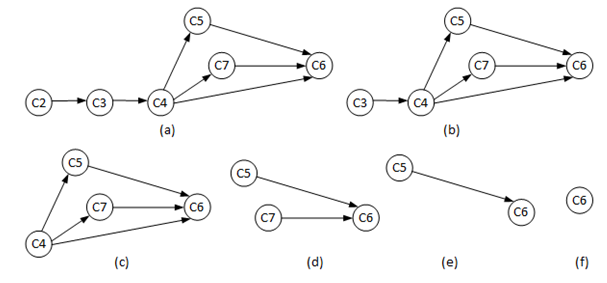
图2 拓扑排序顶点选择过程图示
图1中的课程关系图不存在环路,依据拓扑排序规则进行操作,输出图中的所有顶点,得到了一个拓扑序列。如果进行拓扑排序的图中有环路,操作结束之后,图中仍会有顶点剩余,且剩余的顶点都有前驱。
有环的图不符合拓扑排序原则,拓扑排序针对的是有向无环图。举例说明,图3中的有向环路图,完成子工程C5需要事先完成C4,完成子工程C4需要完成C6,完成子工程C6又需要完成C5,而此时子工程C5正在等待C4执行,这样所有子工程都处于等待状态,无法执行。
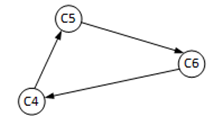
图3 有向环路图
为了实现拓扑排序,对于给定的有向无环图,可以使用邻接表作为其存储结构,并在邻接表头结点中增加一个存放顶点入度的数据域,记作indegree。因为拓扑排序只在意活动之间的制约关系,所以不需要记录弧上的权值。修改后的数据结构定义如下。
//图的数据类型结构定义
typedef struct ArcNode //链表结点
{
int adjvex; //该弧所指向的顶点在数组中的位置
struct ArcNode *next; //指向当前起点的下一条弧的指针
}ArcNode;//弧结点
typedef struct VertexNode
{
int indegree; //存放入度个数
int data; //顶点域,存储顶点信息
ArcNode* firstedge; //指针域,指向顶点链表
}VertexNode,AdjList[MAX_VERTEX_NUM];//头结点
typedef struct
{
AdjList adjList; //邻接表头结点数组
int n, e; //图的顶点数和弧数
}GraphAdjList;//邻接表存储结构定义入度为零的顶点即为没有前驱的顶点,当顶点的入度为零时,将顶点输出,同时将该顶点所有后继顶点的入度减1。为了避免重复检测入度为零的顶点,将入度为零的顶点串成链表,若有顶点入度减为零,将该顶点插入链表尾部;每次需要输出入度为零的顶点时,输出表头的结点,并将其从链表删除。这个链表相当于一个队列链表,记为Q。
前面的章节给出了无向图的邻接表存储,这里使用的图为有向图,并且存储结构略有变化,下面给出使用邻接表存储有向图时的函数实现。
//使用邻接表存储有向图时图的创建
int CreateGraph(GraphAdjList *G) //成功建立返回1,不成功则返回0
{
int i, j, k; int v1, v2; ArcNode *newarc;
printf("\n输入有向图顶点数和弧数vexnum,arcnum:"); //输入顶点数和弧数
scanf("%d,%d", &G->n, &G->n); //输入并判断顶点数和弧数是否正确
if (G->n<0 || G->n<0 || G->n>G->n*(G->n - 1))
{
printf("\n顶点数或弧数不正确,有向图建立失败!\n"); return 0;
}
//① 初始化顶点信息
printf("\n输入 %d 个顶点:", G->n); //输入顶点名称
for (i = 0; i<G->n; i++)
{
scanf("%d", G->adjList[i].data);
}
//② 初始化链表部分信息
for (i = 0; i<G->n; i++) //邻接表初始化
{
G->adjList[i].firstarc = NULL;
G->adjList[i].indegree = 0;
}
//③ 初始化弧的信息
printf("\n\n输入 %d 条边:vi vj\n", G->n); //输入有向图的边
for (k = 0; k<G->n; k++)
{
scanf("%d%d", v1, v2); //v1是弧的起点(先决条件),v2是弧的终点
if (i >= G->n)
{
printf("顶点%s不存在,有向图建立失败!\n", v1); return 0;
}
if (j >= G->n)
{
printf("顶点%s不存在,有向图建立失败!\n", v2); return 0;
}
newarc = (ArcNode*)malloc(sizeof(ArcNode)); //头插法创建顶点链表
newarc->adjvex = j;
if (G->adjList[i].firstarc == NULL)
{
newarc->next = NULL;
G->adjList[i].firstarc = newarc;
}
else
{
newarc->next = G->adjList[i].firstarc->next;
G->adjList[i].firstarc->next = newarc;
}
G->adjList[j].indegree++; //对应顶点入度计数加1
}
printf("\n有向图建立成功!\n");
return 1;
}前面小节的Create()函数中,只初始化了邻接表的顶点信息(顺序表)部分和表结点(链表)部分的表头信息。本节的Create()函数中,除了这两项,还初始化了图中弧的信息。
创建好了图,就可以在图的基础上进行拓扑排序。下面给出有向图的拓扑排序算法。
//拓扑排序,若GL无回路,则输出拓扑排序序列并返回0,有回路则返回-1
int TopologicalSort(GraphAdjList *G)
{
int i, k, count;
int e;
ArcNode *p;
SeqQueue Q = Create(); //定义队列
for (i = 0; i<G->n; i++) //入度为0入队列
if (!G->adjList[i].indegree)
Insert(&Q, i);
count = 0; //初始化变量
printf("\n其中一个拓扑排序序列为:\n");
while (!isEmpty(Q))
{
Del(&Q); //输出入度为零的点
printf("%d ", G->adjList[e].data);
count++; //对输出的顶点计数
//遍历当前点的邻接点
for (p = G->adjList[e].firstarc; p; p = p->next)
{
k = p->adjvex; //邻接点位置
//每个邻接点入度减1后若为零则入队列
if (!(--G->adjList[k].indegree))
Insert(&Q, k);
}
}
printf("\n");
if (count<G->n)
{
printf("\n该有向图有回路,无法完成拓扑排序!\n");
return -1;
}
return 0;
}针对于一个有n个顶点e条边的AOV网图来分析拓扑排序算法:算法中第一个for循环将入度为0的顶点入栈, for循环的时间复杂度为O(n);其后的while循环中,每个顶点进栈出栈各一次,入度减1的操作共执行e次,while循环的时间复杂度为O(e)。所以,整个算法的时间复杂度为O(n+e)。
