图的邻接表存储

图的邻接表存储是一种链式存储与顺序存储相结合的存储结构。邻接表存储法既能保留邻接矩阵存储法的优点，又能很好地解决矩阵存储的缺点。这是因为，这种结构为图中的每一个顶点创建一个链表，链表中的结点为这个顶点的邻接点，这个结点称作表结点或者边结点。同时为每一个顶点的链表设置一个头结点，为了实现随机访问，通常将这些头结点以顺序结构的形式存储。邻接表存储在矩阵存储的基础上实现了存储空间的有效利用。

表结点和头结点的存储结构如图1所示：

图1 表结点和头结点

在表结点中，adjvex域存储与顶点邻接点的编号，nextarc域存储顶点下一个邻接点的地址，info域中存储顶点与该邻接点之间的边的信息（如权值等）。头结点中，vexdata域存储当前链表顶点对应的编号或其它相关信息，firstarc域指向当前顶点对应的第一个邻接点。

图2分别给出了前面介绍的有向网图G1和无向网图G2的邻接表。为了使结构清晰，图2的邻接表示例中将存放数据的info域放在adjvex域和nextarc域之间，如果图中的边不带权，可以省略info域。

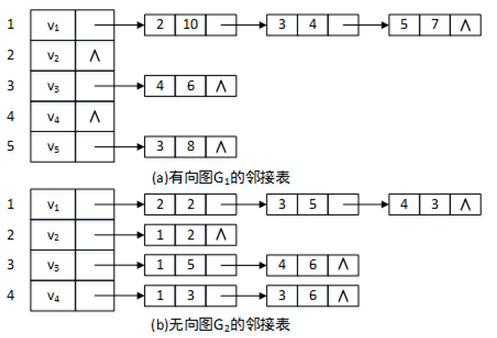
图2 邻接表示例

邻接表存储法的结构定义如下。表中的结点编号、权值等信息仍以int为例。

//邻接表存储法相关结构定义
#define MAX_VERTEX_NUM 100

typedef struct EdgeNode
{
    int adjvex;                //邻接点域，存储该顶点对应编号
    int weight;                //info数据域，存储权值，非网图可省略
    struct EdgeNode* next;    //nextarc指针域
//指向下一个邻接点
}EdgeNode; //表结点

typedef struct VertexNode
{
    int data;                 //顶点域，存储顶点信息
    EdgeNode* firstedge;  //指针域，指向顶点链表
}VertexNode,AdjList[MAX_VERTEX_NUM];//头结点

typedef struct
{
    AdjList adjList;
    int n;                 //图中顶点的数目
    int e;                 //图中边的数目
}GraphAdjList;//邻接表存储结构定义

根据邻接表存储方式的结构和定义，可以得出邻接表存储的以下特点：

● 邻接表存储法表示图时，邻接表不唯一。因为在每一个顶点的单链表中，邻接点的次序可以是任意的，邻接表取决于创建邻接表的算法，与边输入的次序。

● 假设一个图的顶点数目为n，边的数目为e。若是无向图，所需的存储空间为n个表头结点与2e个边结点。若是有向图，所需的存储空间为n个表头结点与e个边结点。而邻接矩阵存储的存储空间总为n2。由此可见，使用邻接表存储比邻接矩阵节省空间。

● 假设顶点为vi。对于无向图，顶点单链表中表结点的数目即为该顶点的度。对于有向图，单链表中表结点的数目是vi的出度；邻接表中adjvex域值为i的表结点的数目是该顶点的入度。

以邻接表存储法为基础创建矩阵，与使用邻接矩阵存储法大致相同，都是为数据元素一一赋值，不同的是，邻接表法的结点空间需要逐一申请，在申请空间的同时进行赋值，可以省去初始化。下面使用C语言代码来实现创建图的算法。

//邻接表法创建无向图
void GreateAdjGraph(GraphAdjList* G)
{
    int i, j, k;
    EdgeNode *e;
    printf("请输入顶点与边的数目，以,分割：");
    scanf("%d,%d", &G->n, &G->e);            //输入顶点与边的数目
    //①头结点（顺序表）部分
    for (i = 0; i < G->n; i++)
    {
        scanf("%d",&G->adjList[i].data);    //输入顶点信息
        G->adjList[i].firstedge = NULL;        //将顶点链表置为空
    }
//②表结点（链表）部分
    for (k = 0; k < G->e; k++)                //建立边表
    {
        printf("输入边：\n");
        scanf("%d,%d", &i, &j);                //输入边
        e = (EdgeNode*)malloc(sizeof(EdgeNode));//为表结点开辟空间
        //表结点赋值
        e->adjvex = j;                        //邻接点序号
        e->next = G->adjList[i].firstedge;    //头插法插入结点j
        G->adjList[i].firstedge = e;

        //头插法插入结点i
        e = (EdgeNode*)malloc(sizeof(EdgeNode));
        e->adjvex = i;
        e->next = G->adjList[j].firstedge;
        G->adjList[j].firstedge = e;
    }
}

GreateAdjGraph()函数基于邻接表法创建矩阵。第①部分是创建和初始化头结点，相当于创建了一个一维数组，并对数组中元素一一赋值，数组元素为顶点相关数据和指针，其时间复杂度只与结点数目有关，为O(n)；第②部分是创建每个顶点的链表，以第①部分中的指针部分作为链表的头部，其时间复杂度只与边的数目有关，为O(e)。所以，对一个有n个顶点和e条边的图来说，使用邻接表法表示图时，创建图的时间复杂度为O(n+e)。

邻接表存储虽然解决了邻接矩阵存储中的问题，但是在获取有向图入度时，需要遍历整个邻接表。这是因为使用邻接表存储时，以弧头为主依次存储了它的邻接点，那么链表中表结点的数目即为顶点的出度。反之，若以弧尾为主，以终点作为头结点使终点相同的顶点链成链表，这样就可以容易获取顶点的入度。我们称以这种方法创建的表为逆邻接表。图2中有向图G1的逆邻接表如下图3所示。

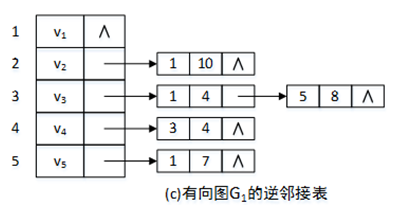
图3 逆邻接表示例