二叉树的非递归遍历
树是递归定义的,因此用递归的算法思想来解决树的遍历等问题比较容易理解,求解代码也比较简洁。但除了递归,树还可以通过非递归遍历。本节以中序遍历为例,讲解二叉树的非递归遍历。,因为在实际开发应用中,中序遍历较之前序遍历与后序遍历更为常用,我们以中序遍历为例来进行讲解。
中序非递归遍历,依然是先访问左子树,然后访问根结点,最后访问右子树。以图1中的二叉树为例,对此树进行非递归中序遍历的分析如下。
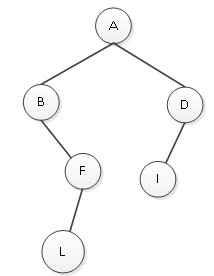
图1 二叉树
此二叉树的非递归遍历同样将二叉树视为三个部分:左子树、根结点、右子树。
第一部分:根结点为A,查看A是否有左子树,有,将A暂存,访问其左子树;
第二部分:A的左子树是以B为根结点的二叉树;
(1)查看B是否有左子树,无,则访问B,输出B;
(2)查看B是否有右子树,有,则访问B的右子树;
(3)B的右子树是以F为根结点的二叉树;
(4)查看F是否有左子树,有,则将F暂存,访问F的左子树;
(5)F的左子树是以L为根结点的二叉树;
(6)查看L是否有左子树,无,则访问L,输出L;
(7)查看L是否有右子树,无,则以L为根结点的二叉树访问完毕;
(8)退回到F结点,访问F结点,输出F;
(9)查看F是否有右子树,无,则以F为根结点的二叉树访问完毕;
(10)B的右子树访问完毕,以B为根结点的二叉树访问完毕,A的左子树访问完毕;
A的左子树访问完毕,则退回到A结点处,访问A,输出A;随后检查A是否有右子树,有,则访问其右子树;
第三部分:A的右子树是以D为根结点的二叉树;
(1)查看D是否有左子树,有,则将D暂存,访问其左子树;
(2)D的左子树是以I为根结点的二叉树;
(3)查看I是否有左子树,无,则访问I,输出I;
(4)查看I是否有右子树,无,则以I为根结点的二叉树访问完毕;
(5)D的左子树访问完毕,则退回到D结点处,访问D,输出D;
(6)查看D是否有右子树,无,则以D为根结点的二叉树访问完毕;
(7)A的右子树访问完毕;
在二叉树的非递归遍历过程中,需要先找到遍历的起点,如先找到根结点A的左子树,如果A的左子树还有左子树,则会继续往下寻找,直到找到没有左子树的结点,以这个结点为起始结点开始访问。
在这个过程中,读者可能会发现,先经过的结点后访问,除非此结点没有左子树,例如结点A,先经过了结点A,但只是把A暂存起来,去访问其左子树,当把A的左子树访问完毕后才回到A结点来访问。而对于后访问到的结点,例如B结点,它也是遍历这棵树的起点,在A结点之后经过却是先被访问。对于暂时不输出的结点,将它们暂存起来,等访问到时再取出。基于上述遍历规律,我们很容易就能想到这与栈处理数据的特点相同,因此可以用栈来解决非递归中序遍历二叉树的问题。
为了让读者更好地理解其遍历过程,以图1为例,结合图解来分析树中各结点的访问及入栈出栈过程。
(1)首先访问根结点A,A有左子树,则A结点入栈,如图2所示。

图2 A结点入栈
(2)A结点入栈后,指针下移,访问A结点的左子树,其左子树是以B为根结点的二叉树。访问结点B,判断B是否有左子树。B没有左子树,输出B,如图3所示。
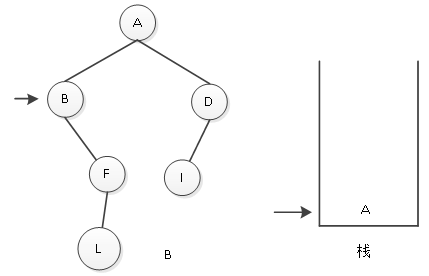
图3 输出结点B
(3)访问B结点后,判断B是否有右子树,有,使指针下移,指向结点F,访问F结点,判断F结点是否有左子树,有,则F结点入栈,如图4所示。
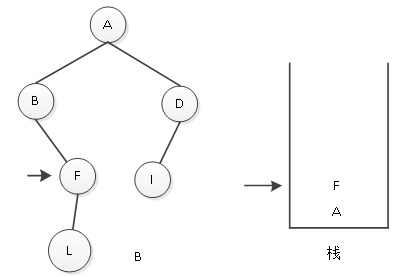
图4 F结点入栈
(4)F结点入栈后,指针下移,遍历其左子树;其左子树是以L为根结点的二叉树,访问L结点,L没有左子树,则访问L,将其输出,如图5所示。
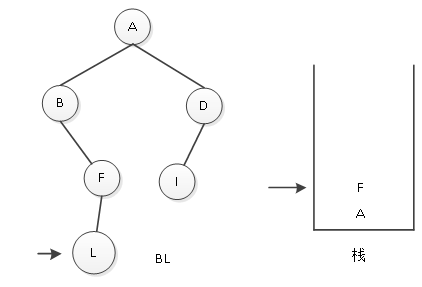
图5 输出L结点
(5)输出L结点后,要访问其右子树,L没有右子树,则表示L结点访问完毕;根据栈顶指针回退到F结点,访问F,将其输出。如图6所示。
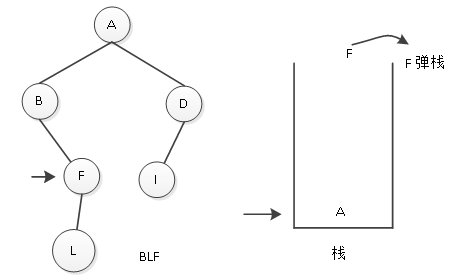
图6 输出F结点
(6)访问完栈顶元素结点后,要访问其右子树,F没有右子树,则根据栈顶指针指示再次回退,结果回退到结点A,访问A结点,将其输出。如图7所示。
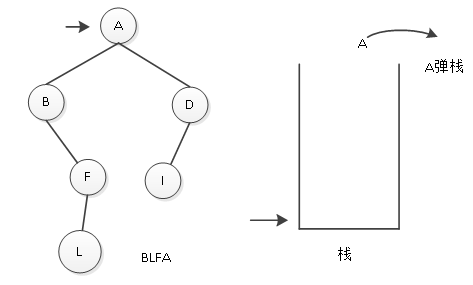
图7 输出A结点
(7)访问完栈顶元素结点A之后,访问其右子树,即遍历D结点,因为D结点有左子树, D结点入栈,如图8所示。
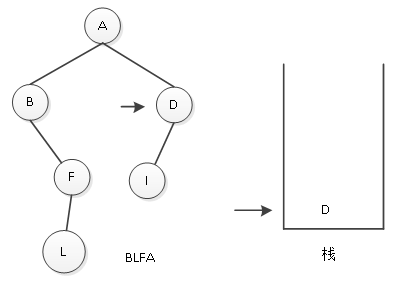
图8 D结点入栈
(8)D结点入栈后,访问其左子树,左子树是以I为根结点的二叉树,而I没有左子树,则访问I结点,将其输出,如图9所示。
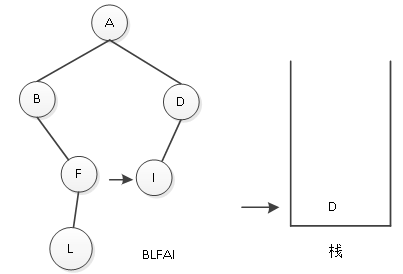
图9 输出结点I
(9)结点I也没有右子树,则根据栈顶指示,回退到结点D,访问D结点,将其输出,如图10所示。
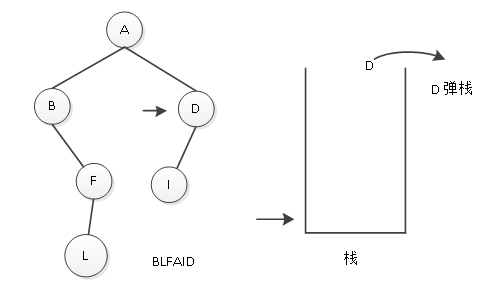
图10 输出结点D
(10)访问D结点后,访问其右子树,D没有右子树,且此时栈已为空,表示树已经遍历完毕。那么图10中“BLFAID”就是其遍历输出结果。
经过上面的讲解及图解,想必读者已经理解了非递归中序遍历的过程,那么在实现相应算法时就比较容易了。其算法代码在接下来的案例中实现,为了让案例代码更完整,这里就不再单独给出算法代码。在遍历过程中用到的栈,在栈中已经学习,此处将前面章节的链式栈稍加修改,用于存储二叉树中的结点,具体如例1所示。
例1
linkstack.h //头文件
1 #ifndef _LINKSTACK_H_
2 #define _LINKSTACK_H_
3
4 //二叉树的结点结构
5 typedef struct BitNode
6 {
7 char data; //数据类型为char
8 struct BitNode* lchild, *rchild;
9 }BitNode;
10
11 //栈的结点结构
12 typedef struct Node * pNode;
13 typedef struct Stack * LinkStack;
14 struct Node //数据结点
15 {
16 BitNode* data; //数据,BitNode结构体类型的指针
17 pNode next; //指针
18 };
19
20 struct Stack //此结构记录栈的大小和栈顶元素指针
21 {
22 pNode top; //栈顶元素指针
23 int size; //栈大小
24 };
25
26 LinkStack Create(); //创建栈
27 int IsEmpty(LinkStack lstack); //判断栈是否为空
28 int Push(LinkStack lstack, BitNode* val); //元素入栈
29 pNode getTop(LinkStack lstack); //获取栈顶元素
30 pNode Pop(LinkStack lstack); //弹出栈顶元素
31
32 #endiflinkstack.c //算法实现
33 #include "linkstack.h"
34 #include <stdio.h>
35 #include <stdlib.h>
36
37 LinkStack Create() //创建栈
38 {
39 LinkStack lstack = (LinkStack)malloc(sizeof(struct Stack));
40 if (lstack != NULL)
41 {
42 lstack->top = NULL;
43 lstack->size = 0;
44 }
45 return lstack;
46 }
47
48 int IsEmpty(LinkStack lstack) //判断栈是否为空
49 {
50 if (lstack->top == NULL || lstack->size == 0)
51 return 1;
52 return 0;
53 }
54
55 int Push(LinkStack lstack, BitNode* val)
56 {
57 pNode node = (pNode)malloc(sizeof(struct Node)); //为元素val分配结点
58 if (node != NULL)
59 {
60 node->data = val;
61 node->next = getTop(lstack); //新元素结点指向下一个结点,链式实现
62 lstack->top = node; //top指向新结点
63 lstack->size++;
64 }
65 return 1;
66 }
67
68 pNode getTop(LinkStack lstack) //获取栈顶元素
69 {
70 if (lstack->size != 0)
71 return lstack->top;
72 return NULL;
73 }
74
75 pNode Pop(LinkStack lstack) //弹出栈顶元素
76 {
77 if (IsEmpty(lstack))
78 {
79 return NULL;
80 }
81 pNode node = lstack->top; //node指向栈顶元素
82 lstack->top = lstack->top->next; //top指向下一个元素
83 lstack->size--;
84 return node;
85 }main.c //测试文件
86 #include <stdio.h>
87 #include <stdlib.h>
88 #include "linkstack.h"
89
90 //寻找遍历起始结点
91 BitNode* GoFarLeft(BitNode* T, LinkStack ls)
92 {
93 if (T == NULL)
94 return NULL;
95 while (T->lchild != NULL) //左子树不为空,就一直往下寻找
96 {
97 Push(ls,T);
98 T = T->lchild;
99 }
100 return T;
101 }
102
103 //非递归中序遍历函数
104 void MyOrder(BitNode* T)
105 {
106 LinkStack ls = Create(); //创建栈
107 BitNode* t = GoFarLeft(T, ls); //寻找遍历起始结点
108 while (t != NULL)
109 {
110 printf("%c", t->data); //打印起始结点的值
111 //若结点有右子树,则访问其右子树
112 if (t->rchild != NULL)
113 t = GoFarLeft(t->rchild, ls); //寻找右子树中的起始结点
114 else if (!IsEmpty(ls)) //如果栈不为空
115 {
116 t = getTop(ls)->data; //回退到栈顶元素结点
117 Pop(ls); //栈顶元素弹出
118 }
119 else
120 t = NULL;
121 }
122 }
123 int main()
124 {
125 BitNode nodeA, nodeB, nodeD, nodeF, nodeI, nodeL; //创建6个结点
126 //将结点都初始,这样可以保证没有孩子的结点相应指针批向空
127 memset(&nodeA, 0, sizeof(BitNode));
128 memset(&nodeB, 0, sizeof(BitNode));
129 memset(&nodeD, 0, sizeof(BitNode));
130 memset(&nodeF, 0, sizeof(BitNode));
131 memset(&nodeI, 0, sizeof(BitNode));
132 memset(&nodeL, 0, sizeof(BitNode));
133 //给结点赋值
134 nodeA.data = 'A';
135 nodeB.data = 'B';
136 nodeD.data = 'D';
137 nodeF.data = 'F';
138 nodeI.data = 'I';
139 nodeL.data = 'L';
140 //存储结点之间的逻辑关系
141 nodeA.lchild = &nodeB; //A结点左孩子是B
142 nodeA.rchild = &nodeD; //A结点的右孩子是D
143 nodeB.rchild = &nodeF; //B结点的右孩子是F
144 nodeF.lchild = &nodeL; //F结点的左孩子是L
145 nodeD.lchild = &nodeI; //D结点的左孩子是I
146
147 printf("二叉树构建成功!\n");
148
149 printf("非递归中序遍历:");
150 MyOrder(&nodeA);
151
152 printf("\n");
153 system("pause");
154 return 0;
155 }运行结果如图11所示。

图11 例1运行结果
例1的头文件linkstack.h中定义了二叉树结点结构与栈的存储结点结构。注意:在栈的存储结点结构中,数据域的数据类型为BitNode*类型,即存储的是二叉树结点指针。在树的遍历过程中只用到栈的创建、入栈、获取栈顶元素、出栈、判断栈空的操作,因此只保留了Create()、Push()、getTop()、Pop()与IsEmpty()五个函数。
在linkstack.c文件中,函数的实现与第三章中例3-2中的实现相同,基本没有作任何改动,只是Push()函数的第二个参数变了BitNode*类型。
在main.c测试文件中,代码104-122行实现了非递归中序遍历算法MyOrder();
代码106行调用Create()函数创建了一个栈;
107行代码调用GoFarLeft()函数寻找遍历起始结点,关于GoFarLeft()函数见代码91-101行,函数实现较简单,不再细说;
代码108-121行是该算法的核心部分:如果起始结点不为空,则打印起始结点值;然后判断结点右子树是否为空,不为空则在右子树中寻找起始结点;如果右子树为空,则判断栈是否为空,如果栈不为空,则根据栈顶指示回退到栈顶元素结点,然后弹出栈顶元素;如果结点右子树为空且栈也为空,则表示遍历完成,令t=NULL即可。
本案例中,大量代码在其他案例中都有出现,但为了使读者能够完整的接触到非递归遍历过程的代码,本案例将树的构建、栈的实现等又重新给出,读者在学习时要认真练习并理解。
