二叉树的性质

二叉树具有许多重要特性，下面将一一讲解。

性质1：在二叉树的第i层上至多有2i-1个结点（i> 0）。

对于这个性质，利用数学归纳法很容易获得：

i=1，有21-1 = 1个结点；

i=2，有22-1 = 2个结点；

i=3，有23-1 = 4个结点；

……

注意：这里指的是最多的结点。

性质2：深度为k的二叉树至多有2k-1个结点（k>0）。

性质2也可以用数学归纳法来证明，这个性质在讲满二叉树时也曾提及，一棵深度为k的二叉树，在结点数达到2k-1个时，一定是一棵满二叉树。

性质3：对于任何一棵二叉树，若度为2的结点数有n2个，则叶子数（n0）必定为n2+1（即n0 = n2 + 1）。

为了证明此性质，我们假设二叉树中度为1的结点个数为n1，则二叉树中所有结点的总数n=n1+n2+n0；除去根结点外，度为1的结点会延伸出一个孩子结点，度为2的结点会延伸出2个孩子结点，那么二叉树总的结点数也可以表示为n=n1+2n2+1；由n= n1+n2+n0 = n1+2n2+1，得出n0 = n2+1。

性质4：具有n个结点的完全二叉树，它的深度必为⌊log2n⌋ + 1。

假设完全二叉树的深度为k，结点数为n，那么一定小于同样深度满二叉树的结点数2k-1；但又大于2k-1-1（深度为k-1的满二叉树）；即

2k-1-1<n<=2k-1

因为n为正整数，上式可表述为2k-1<=n<2k-1；于是k-1<=log2n<k，因为k是整数，所以k = ⌊ log2n⌋ +1。

性质5：若对完全二叉树中的结点从上至下、从左至右编号，则编号为i（1<=i<=n）的结点，其左孩子编号必为2i，其右孩子编号必为2i+1；其双亲编号必为i/2（i = 1时除外）；编号规则如图1所示。

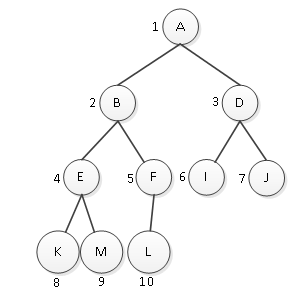
图1 完全二叉树的编号规则

如图1所示，假如第k层中编号为i的元素在本层中位于该元素之前的元素有x个，在本层中位于该元素之后的元素有y个，如图2所示。

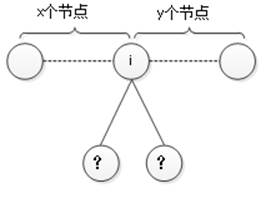
图2 编号为i的结点

那么它左右孩子编号为多少呢？

根据完全二叉树的性质可知，完全二叉树的第k-1层有2k-1-1个元素，第k层有2k-1个元素，则第k层中编号为i的元素在本层中位于该元素前面的元素个数为：x=i-1-(2k-1-1)=i-2k-1，在本层中位于该元素后面的元素个数为：y=2k-1-i。

因为y为第k层中编号为i的元素之后的元素个数， x个结点会产生2x个子结点，所以编号为i的元素与其左孩子之间的元素个数为y+2x。

综上，其左孩子编号为：

i+y+2x+1 = i+2k-1-1-x+2x+1=i+2k-1+x=i+2k-1+i+ 2k-1=2i

则其右孩子编号是：

2i+1

同样，对于左右孩子，其父结点编号也必然为⌊i/2⌋。