置换-选择排序
减小初始归并段的数量可以减少归并轮数。
假设待排序的文件中共有n条记录,每个归并段中包含l条记录,按照一般的求解思路,初始归并段的数量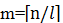 。n的数值显然是固定不变的,那么只能从l着手去减小m的值。按照前面对外排序的分析,l受内存可用容量限制,若要突破这个限制增大l,就要探索一种新方法。置换-选择排序就是符合要求的新方法。
。n的数值显然是固定不变的,那么只能从l着手去减小m的值。按照前面对外排序的分析,l受内存可用容量限制,若要突破这个限制增大l,就要探索一种新方法。置换-选择排序就是符合要求的新方法。
置换-选择排序基于选择排序,在生成初始归并段时,通过关键字的比较,从若干条记录中选择一个关键字最小(或最大)的记录,同时在此过程中进行数据的输入和输出,最后可生成若干个长度不等,各自有序的子文件。
设待排序文件为F,内存可用容量WA中可存储w条记录,归并段的编号为i,则置换-选择排序的基本步骤如下:
(1)从待排序文件F中读w条记录到内存中,设置归并段编号i=1;
(2)从存在于WA的w条记录中选出关键字最小的记录,记为Rmin;
(3)将记录Rmin输出到文件Fi中;
(4)若F不为空,从F中输入下一条记录到WA中;
(5)从WA所有关键字比记录Rmin关键字大的记录中,选择关键字最小的记录,使用Rmin记录该条记录;
(6)重复步骤(3)~(5),直到WA中不能选出新的Rmin记录为止,此时初始归并段Fi生成完毕;
(7)使i=i+1,重复步骤(2)~(6),生成下一个归并段,直到WA为空,由此得到所有归并段。
举例说明置换-选择排序生成初始归并段的过程:假设当前待排序的磁盘文件F中共有16条记录,记录的关键字分别为{85,11,21,92,24,12,10,26,52,27,8,15,63,49,79,17},设内存可用容量WA最多可存储5条记录,则使用置换-选择排序生成初始归并段的过程如表1所示。
表1 初始归并段生成过程
| 读入记录 | WA | Rmin | i | 归并段 |
|---|---|---|---|---|
| 85,11,21,92,24 | 85,11,21,92,24 | 11 | 1 | F1:{11} |
| 12 | 85,12,21,92,24 | 12 | 1 | F1:{11,12} |
| 10 | 85,10,21,92,24 | 21 | 1 | F1:{11,12,21} |
| 26 | 85,10,26,92,24 | 24 | 1 | F1:{11,12,21,24} |
| 52 | 85,10,26,92,52 | 26 | 1 | F1:{11,12,21,24,26} |
| 27 | 85,10,27,92,52 | 27 | 1 | F1:{11,12,21,24,26,27} |
| 8 | 85,10,8,92,52 | 52 | 1 | F1:{11,12,21,24,26,27,52} |
| 15 | 85,10,8,92,15 | 85 | 1 | F1:{11,12,21,24,26,27,52,85} |
| 63 | 63,10,8,92,15 | 92 | 1 | F1:{11,12,21,24,26,27,52,85,92}√ |
| 49 | 63,10,8,49,15 | 8 | 2 | F2:{8} |
| 79 | 63,10,79,49,15 | 10 | 2 | F2:{8,10} |
| 17 | 63,17,79,49,15 | 15 | 2 | F2:{8,10,15} |
| 63,17,79,49, | 17 | 2 | F2:{8,10,15,17} | |
| 63, ,79,49, | 49 | 2 | F2:{8,10,15,17,49} | |
| 63, ,79, , | 63 | 2 | F2:{8,10,15,17,49,63} | |
| , ,79, , | 79 | 2 | F2:{8,10,15,17,49,63,79}√ | |
| F1:{11,12,21,24,26,27,52,85,92} F2:{8,10,15,17,49,63} |
经过表9-4中的过程,文件F最终生成了两个初始归并段,分别为:F1:{11,12,21,24,26,27,52,
85,92};F2:{8,10,15,17,49,63}。
在使用基本方法为文件F生成归并段时,归并段最多包含5条记录,而使用置换-选择方法时,归并段中包含的记录有效增加。那么使用置换-选择排序方法到底能使初始归并段的长度增加多少呢?答案是:如果输入文件中的记录按其关键字随机排列,那么使用置换-选择排序方法得到的初始归并段的平均长度为内存工作区大小的2倍。这个问题由E·F·Moore在1961年通过将置换-选择排序与扫雪机相类比给出解答。
假设一台扫雪机在一条环形路面上匀速前进,进行扫雪工作,雪花匀速下降(即每小时落到地面上的雪量相等),并且均匀地落在扫雪机的前、后路面上。显然,在某个时刻之后,整个系统达到平衡状态,路面上的积雪总量保持不变,且在任何时刻,路面上的积雪都形成一个均匀的斜面,靠近扫雪机前端的积雪最厚,设其深度为h;扫雪机刚刚扫过的路面积雪最薄,其深度为0,若将环形路面伸展开来,路面积雪的状态如图1所示。假设环形路面的长度为l,此刻路面上积雪的总体积为m,则m=hl/2,所以hl=2m。由于扫雪机在任一时刻扫走的雪深度均为h,所以扫雪机在环形路上走一圈扫掉的积雪体积为hl,也就是2m。
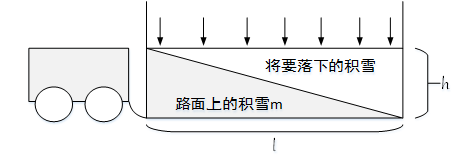
图1 环形路上平衡状态下扫雪机扫雪示意图
将在内存中进行置换-选择排序算法的情形与扫雪机类比:内存中已经有的记录数量相当于环形路面上已经存在的积雪的总量,从内存输出的记录相当于扫雪车扫掉的积雪,从输入文件读入内存中的记录相当于新落到路面上的雪。对于新读入的数据,凡是关键字比当前关键字大的记录,都要从内存中输出,输出的这一部分相当于落在扫雪车前面的雪;而关键字比当前关键字小的记录,将会在下一个归并段生成的时候输出,相当于落在扫雪车后的雪,在扫雪车下一次开到这里的时候才会被扫掉。因为文件中的记录是按其关键字随机排列的,所以假设读入记录中的关键字比当前关键字大或者小的概率相同,这相当于雪是均匀地落在扫雪车的前面或后面的路面上。一旦内存中记录的关键字均小于当前关键字,说明一个初始归并段已经生成,这相当于扫雪车已经沿着环形路走了一圈。初始归并段所包含的记录数量相当于扫雪车走一圈扫掉的雪的总量,设内存容量为m,则初始归并段的平均长度为2m。
