简单选择排序

简单选择排序是最基础的一种选择排序，这种排序方法严格贴合选择排序基本思想。与直接插入排序类似，简单选择排序也可以将序列视为两部分，只是直接插入排序初始的有序序列有一个元素，简单选择排序初始的整个序列都视为待排序序列，有序序列为空。

直接插入排序依次选择待排序序列中的元素，并将其插入有序序列的合适位置，而简单选择排序是依次为序列中的每个位置，选择合适的元素。

如图1所示，图中待排序序列为arr[2]~arr[9]，在此之前，算法已经为0号位置和1号位置依次选择了最大值9和次大值8作为其存放的元素。

从arr[2]~arr[9]，首部位置为arr[2]，通过比较选择其中的最大值，也就是arr[8]=7，交换arr[2]与arr[8]，将本轮的最大元素放置在无序序列的首部，本轮排序结束。

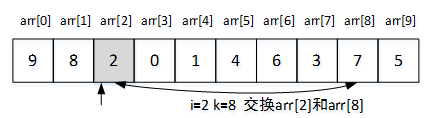
图1 简单排序操作图示

其中的核心操作在于最值的选择。在选择的过程中，需要一个中间变量max来记录当前找到的最小值对应的下标。以图2中的序列为例，该序列将要进行第3轮选择排序，也就是要为arr[2]寻找合适的元素，具体操作如下：

（1）从arr[2]开始寻找，初始化max=2；

（2）使arr[max]依次与其之后数据arr[j]进行比较：

a) 若arr[max]>arr[j]，继续往后比较；

b) 若arr[max]<arr[j]，使max= j；

（3）j=j+1。

（4）循环执行步骤(2)(3)，直到j<n不成立为止（n为序列中元素个数，对于arr[]，n=10）。此时max记录的值为arr[2]~arr[9]中的最大值对应的下标。交换arr[2]与arr[max]。

本轮排序结束，下轮待排序序列为arr[3]~arr[9]，将为arr[3]寻找合适的元素。

综上所述，若要使用简单选择排序使数组arr[n]成为一个降序序列，使用i记录当前需要选择最值的位置；使用max记录当前已参与比较的元素中最大值对应的下标，其操作过程如下：

（1）在第m轮比较中，i=m-1，使max=i，即记录当前需要选择最大值的位置，同时初始化j=i+1；

（2）比较arr[max]与arr[j]：

a) 若arr[max]>arr[j]，不进行赋值操作；

b) 若arr[max]<arr[j]，使max= j；

（3）j=j+1。

（4）循环执行步骤(2)(3)，直到j<n不成立。此时max记录的值为arr[i]~arr[n-1]中的最大值对应的下标，交换arr[i]与arr[max]。

（5）i=i+1，若i<n-1成立，重复上述步骤(1)~(4)，进入下一轮循环。

下面以图2中的int型数组arr[10] ={2, 0, 9, 8, 1, 4, 6, 3, 7, 5}为例，演示使用简单选择排序使其转化为降序序列的过程。

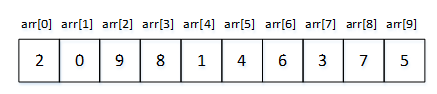
图2 原始arr[]序列

（1）在第一轮排序中，i=1-1=0，初始化中间变量max为0，j=i+1，同时使arr[max]与arr[0]之后的数据逐个比较：

j=1，j<10，arr[max]>arr[1]成立，max值不变，j++；

j=2，j<10，arr[max]>arr[2]不成立，max=2，j++；

j=3，j<10，arr[max]>arr[3]成立，max值不变，j++；

……

j=9，j<10，arr[max]>arr[9]成立，max值不变，j++；

j=10，j<10不成立，循环结束。在本轮循环中，当j为2时，max被更新为2，之后的比较中max值均未发生改变，所以交换arr[2]与arr[0]。

本轮循环结束，排序结果如图3所示。

图3 第一轮选择排序结果

（2）之后进行第二轮排序。i=2-1=1，初始化中间变量max为i，j=i+1=2，使用tmp与arr[i]之后的数据逐个比较：

j=2，j<10，arr[max]>arr[2]不成立，max =2，j++；

j=3，j<10，arr[max]>arr[3]不成立，max=3，j++；

j=4，j<10，arr[max]>arr[4]成立，max不变，j++；

……

j=9，j<10，arr[max]>arr[j]成立，max值不变，j++；

j=10，j<10不成立，循环结束。在本轮循环中，当j为3时，max被更新为3，之后的比较中max值均为发生改变，所以交换arr[3]与arr[1]。

本轮循环结束，排序结果如图4所示。

图4 第二轮选择排序结果

之后的排序都遵从一二两轮的规律，这里就不再赘述。

​ 根据以上分析可得，对于一个有n条记录的序列，第i轮排序需要比较n-i次，经过n-1轮比较之后，可以获得一个有序序列。

​ 下面给出简单选择排序算法的代码实现。

//简单选择排序
void SelectSort(int arr[], int n)
{
    int i, j, max;
    for (i = 0; i < n; i++)
    {
        max = i;            //定义当前下标为最小值下标
        for (j = i; j < n; j++)    //查找最大值，并记录其下标
        {
            if (arr[max] < arr[j])
                max = j;
        }
        //若i不等于max，说明找到最大值，进行交换
        if (i != max)
            swap(&arr[i], &arr[max]);
    }
}

简单选择排序算法包含一个简单的双层循环，其时间复杂度为O(n2)。该算法在进行排序的时候可能会改变两个键值相同记录的顺序，比如对于数据{7,7,2}，使其成为一个升序序列，第一个7在一轮选择排序之后会被换到第三个位置，两个7的先后次序就发生了变化。所以简单选择排序算法不是一个稳定的算法。