循环队列

为了解决顺序队列中的假“溢出”现象，充分利用数组的存储空间，可以将顺序队列的头尾相连，构成一个循环队列，循环队列一般都是用数组来实现的。将循环队列假想为一个环状的空间，如图1所示。

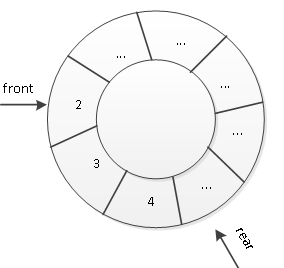
图1 循环队列

在循环队列中，front与rear都是可以循环移动的，当队空时，front =rear成立；当队满时，front =rear也成立。因此显然不能只凭front = rear来判断队空还是队满。

为了解决这个问题，在循环队列中有一个约定：少用一个元素空间，当队尾标识的rear在队头标识front的上一个位置时，队列为满。此时，判断队空和队满的条件分别如下：

队空时：front ==rear为真。

队满时：(rear + 1)%MAXSIZE == front为真。

其中，MAXSIZE是队列容量的大小，两种情况下队列中指针的状态如图2所示。

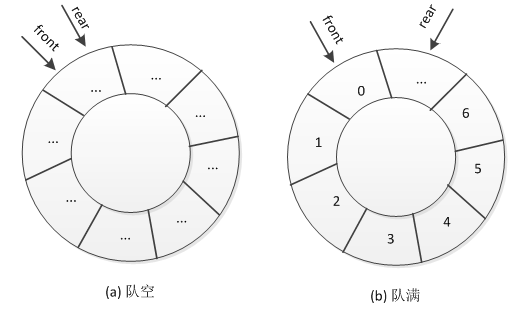
图2 循环队列的队空与队满状态

循环队列中 front和rear的移动不再是简单的加一，因为是循环的，可能原本指在末尾，前进一个单位就是又一个循环的开始，所以每次移动都要对队列容量MAXSIZE取模：front = (front + 1) %MAXSIZE，rear = (rear + 1) % MAXSIZE。

在循环队列中，求队列的长度也不仅仅是rear与front相减这么简单，因为，rear的值有可能比front小，这样相减结果是负值，显然不对。在求循环队列的长度时，都是用rear加上队列容量，减去front的值后，再对容量取模：(rear + MAXSIZE - front) % MAXSIZE。

循环队列与顺序队列的实现相似，除了队空队满的判断，以及队列长度求算与顺序队列稍有区别外，其他并无不同。我们不再对循环队列的基本操作一一实现，只实现入队、出队两个核心操作。

入队代码如下：

void Insert(CirQueue Cq, int val) // 入队
{
    if ((Cq->rear + 1) % MAXSIZE == Cq->front) //判断队满的条件
    {
        printf("队列已满，无法再插入元素！\n");
        return;
    }
    if (IsEmpty(Cq)) //如果队列为空
    {
        Cq->front = Cq->rear = 0;
        Cq->data[Cq->rear] = val;
        Cq->rear++;
    }
    else
    {
        Cq->data[Cq->rear] = val;
        Cq->rear = (Cq->rear + 1) % MAXSIZE;
    }
}

在入队时，与顺序队列相同，先判断队列是否已满，如果已满则无法再插入元素；如果队列未满，判断队列是否是空的，如果为空，front与rear都置于0，在0位置插入元素，rear向后移动；如果不为空，将元素插入到rear的位置，rear向后移动。注意：rear移动是(Cq->rear + 1) % MAXSIZE。

出队代码如下：

int Del(CirQueue Cq)// 出队
{
  if (IsEmpty(Cq))
  {
​    printf("队列为空，无元素可出队！\n");
​    return 0;
  }
  int temp = Cq->data[Cq->front];
  Cq->front = (Cq->front + 1) % MAXSIZE;
  return temp;
}

元素出队时，也和顺序队列相同，先判断队列是否为空，如果为空，则无元素可出；如果不为空，则将front位置的元素弹出，然后front向后移动，下一个元素成为新的队头元素。注意：front移动的距离也是(Cq->front + 1) % MAXSIZE。

限于篇幅，其他操作不再详细实现，读者可以在理解了循环队列的基础上，参照顺序队列来实现其余操作，然后完成测试，也可以到博学谷网站下载完整代码以供参考。

多学一招：优先队列

在某些情况下，简单的先进先出原则是无法满足使用需求的，例如，在邮局办理业务时，残疾人要比普通人有一定的优先权，当有业务员空闲时，会优先给残疾人办理业务；在红灯时，救护车、警车也可不用排队等待而优先通过。此类情况下，就需要使用优先队列（Priority Queue）。

所谓优先队列，就是根据元素的优先级以及在队列中的当前位置决定元素出队的顺序。优先队列是0个或多个元素的集合，每个元素都有一个优先权值，元素的优先权越高，则会越早出队（被操作）。

优先队列的操作与顺序队列、链式队列的操作并无区别，只是在出队时是按某一优先权来确定哪个元素出队，这个优先权可以是系统指定也可以是自定义的。

优先队列可以用顺序表、链表实现，还可以用堆来实现，比如二叉堆、左式堆等，这些堆在底层是以二叉树的形式来实现的，它常常与排序算法等结合起来。关于二叉树及堆的排序我们将在后面章节进行讲解。