斐波那契查找

斐波那契查找也是对折半查找的一种优化。在折半查找中，无论要查找的数据是偏大还是偏小，一组数据总是从中间一分为二，这样未必合理。插值查找对它做了优化，但只适用于数据分布均匀的查找表，限制性较强。本节再来学习一种针对有序表的查找算法—斐波那契查找，该算法利用了黄金分割的原理。

在C语言中我们学习过斐波那契数列，在斐波那契数列中，有一个特性，对于任一角标k(k>=2)，F[k]=F[k-1]+F[k-2]，即后边每一个数都是前两个数的和。而且随着数列的递增，前后两个数的比值会越来越接近黄金分割数—0.618，利用这个特性，就可以将黄金比例运用到查找技术中。现在有一组斐波那契数列F，如图1所示。

图1 斐波那契数列

但是首先要明确一点：如果一个有序表的元素个数为n，并且n正好是某个斐波那契数减1，即满足n=F[k]-1时，才能使用斐波那契查找。如果元素个数n不满足这个关系，那么需要将查找表扩展，直到n满足这个关系 。假如现在有一组数据组成的查找表arr，如图2所示。

图2 查找表arr

数组arr有10个元素，即n=10，在斐波那契数列F中，没有数据满足n=F[k] -1，最近的是数据13-1=12，那么就把数据arr由10个元素扩展到12个，用最后一个元素来扩展另外两个空间。扩展后的数组arr如图3所示。

图3 扩展后的查找表arr

扩展元素的代码实现如下所示：

for (int i = n; i < F[k] - 1; i++)
​    arr[i] = arr[n-1];

在这个案例中，n的值为10，k的值应为7，F[k]=F[7]=13。查找表arr被扩充为F[7]-1=12个元素。

查找表arr的长度其实也很好估算，假如定义了n=7个元素的数组，那么在斐波那契数列中，8-1=7，8对应的角标为6，即7=F[6]-1，满足n=F[k]-1的关系，不必扩展；如果定义的查找中有n=25个元素，那么F[9]-1=34-1=33，那么要把arr从25个元素扩展到33个。这就是刚开始说的n与F[k]-1的关系。

在二分查找中，分割点mid=(begin+last)/2，而在斐波那契查找中分割点mid=begin+F[k-1]-1。通过上面的学习我们知道，查找表arr现在的元素个数为F[k]-1，mid将查找表分成了两部分，左边的长度为F[k-1]-1，则右边的长度为F[k]-1-(F[k-1]-1)=F[k-2]-1。如图4所示。

图4 查找表arr元素分布

接下来我们就通过斐波那契查找法来查找arr中是否存在元素102，其过程如下所示：

（1）通过上述分析得知：arr由10个元素扩充到12个，此时k=7，则mid=begin+F[k]-1=0+F[7-1]-1=7，也就是arr从角标7处一分为二，如图5所示。

图5 mid=7

（2）求得mid=7，如果arr[mid]值比key=102小，则begin往后移：

begin=mid+1;k=k-2;

如果arr[mid]值比key=102大，则last往前移：

last=mid-1;k=k-1;

​ 而此时arr[mid]=arr[7]=90，它要比key值小，则重新为begin和key赋值，begin=mid+1=7+1=8; k=k-2=7-2=5; 则再次求得mid=begin+F[k-1]-1=8+F[5-1]-1=8+3-1=10（原先arr已经由10个元素扩展到12个），即从角标10处将arr一分为二，如图6所示。

图6 mid=10

（3）mid=10,则arr[mid]=130，比key值大，则last往前移，last=mid-1=10-1=9; k=k-1=5-1=4;则再次求得mid=begin+F[k-1]-1=8+F[4-1]-1=8+2-1=9，则从角标为9处将arr一分为二，如图7所示。

图7 mid=9

（4）mid=9，则arr[mid]=130，大于key值，则last往前移，last=mid-1=9-1=8; k=k-1=4-1=3; 则再次求得mid=begin+F[k-1]-1=8+F[3-1]-1=8+1-1=8，则从角标8处将arr一分为二，如图8所示。

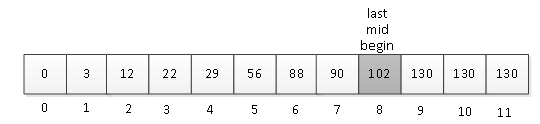
图8 mid=8

此时，arr[mid]=arr[8]=102，元素查找成功。

通过了上面的学习，斐波那契查找的算法实现也简单了，其代码如下所示：

int F[] = {0,1,1,2,3,5,8,13,21,34,55,89}; //当然也可以构造别的斐波那契数列
int Fibonacci_Search(int *arr, int n, int key)  
{
    int begin = 0;
    int last = n - 1;

    int k = 0;
    while (n>F[k] - 1)                        //计算n位于斐波那契数列的位置  
        ++k;
    for (int i = n; i < F[k] - 1; i++) //扩展赋值
        arr[i] = arr[n - 1];

    while (begin <= last)
    {
        int mid = begin + F[k - 1] - 1;
        if (key<arr[mid])
        {
            last = mid - 1;
            k -= 1;
        }
        else if (key>arr[mid])
        {
            begin = mid + 1;
            k -= 2;
        }
        else
        {
            if (mid<n)
                return mid;             //若相等则说明mid即为查找到的位置  
            else
                return n - 1;         //若mid>=n则说明是扩展的数值,返回n-1  
        }
    }
    return -1;
}

关于斐波那契查找， 如果要查找的记录在右侧，则左侧的数据都不再判断，不断反复进行下去，对处于当中的大部分数据，其工作效率要高一些。所以尽管斐波那契查找的时间复杂度也为O(logn)，但就平均性能来说，斐波那契查找要优于折半查找。可惜如果是最坏的情况，比如这里key=1，那么始终都处于左侧在查找，则查找效率低于折半查找。

还有关键一点，折半查找是进行加法与除法运算的（mid=(low+high)/2），插值查找则进行更复杂的四则运算（mid = low + (high - low) * ((key - a[low]) / (a[high] - a[low]))），而斐波那契查找只进行最简单的加减法运算（mid = low + F[k-1] - 1），在海量数据的查找过程中，这种细微的差别可能会影响最终的效率。