什么是线索二叉树

通过某种遍历方式遍历一棵二叉树，根据得到的结点序列，可以很清楚地知道任意一个结点的前驱和后继。例如以中序遍历方式遍历图1中的二叉树：

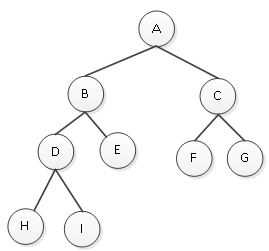
图1 二叉树

中序遍历结果为HDIBEAFCG，由此可知在中序遍历时，D结点的前驱是H，后继是I；F结点的前驱是A，后继是C；通过遍历之后的结果，可以很清楚的知道任意一个结点的前驱结点和后继结点。

但是这是建立在已知遍历结果的基础上的，如果每次需要知道某一个结点的前驱或后继都要重新遍历二叉树，将会非常浪费时间。

可能有读者会说，在二叉链表示法中，结点结构增加了两个指针：lchild和rchild，通过这两个指针可以很轻易的找到结点的左右孩子；而在三叉链表示法中还可以通过parent指针找到结点的父结点……但要注意：孩子结点与后继结点并非同一个概念，父结点与前驱结点也并非同一个概念。孩子结点、父结点与前驱结点、后继结点没有什么联系。

如果在结点结构中再增加两个指针分别指向结点的前驱与后继，那么空间利用率会降低。不过，通过分析二叉链表示法可以发现，结点结构中的指针域并未完全被利用，即有好多空指针域存在。例如图6-59中的二叉树用二叉链表示时就会有许多空指针域，如图2所示。

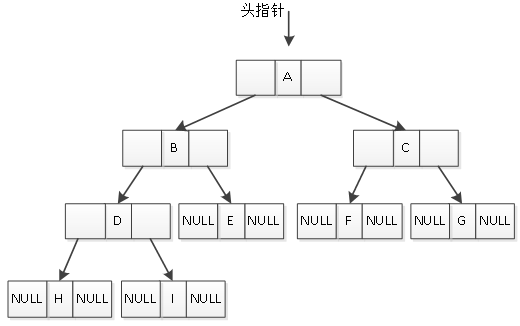
图2 二叉链表存储

在这棵树的二叉链表示法中，一共有18个指针域，但有10个指针域都是空的。一个有n个结点的二叉链表有2n个指针，除了根结点外，每个结点都会有一个从父结点指向该结点的指针，因此一共使用了n-1个指针，那么空指针的个数为2n-(n-1)=n+1个。这些存储空间没有存储任何数据。

综上所述，可以考虑利用这些空指针来存储结点在某种遍历顺序下前驱结点和后继结点的地址。例如，用E的空闲指针lchild来存储其前驱结点B的地址，空闲的rchild来存储其后继结点A的地址；通常把这种指向前驱和后继的指针称为线索，带有线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树。

为图2中的二叉树添加线索：空指针域中的lchild都指向它的前驱结点，rchild都指向它的后继结点，结果如图3所示。

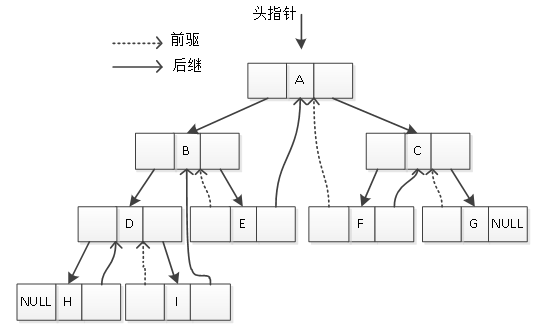
图3 空指针域指向结点的前驱后继结点

在图3中，虚线单箭头指向结点的前驱结点，实线单箭头指向结点的后继结点，这样很容易就能找出各结点的前驱及后继结点，如I结点的前驱为D，后继为B。

但是如何判断某一个结点的lchild是指向其左孩子还是指向其前驱结点？rchild是指向其右孩子还是其后继结点呢？这里需要做一个区分标志，因此在结点结构中可以增加两个标志域：ltag和rtag。这两个标志域设置为取值为0或1的布尔变量，其占用内存空间要远小于再额外分配两个指针变量，C语言中没有布尔类型，只能用int类型的0和1来代替，但在其他高级语言中，都有布尔变量，相对于增加两个指针来说，空间消耗较低。增加了ltag和rtag的结点结构如图4所示。

图4 线索二叉树结点结构

当ltag=0时，结点的lchild指向其左孩子；当ltag=1时，结点的lchild指向其前驱结点（线索）；

当rtag=0时，结点的rchild指向其右孩子；当rtag=1时，结点的rchild指向其后继结点（线索）。

线索二叉树结点结构定义如下所示：

typedef struct BiThrNode  //二叉线索存储结点结构 
{
  char data;   //结点数据 
  struct BiThrNode *lchild, *rchild; //左右孩子指针 
  int  LTag;
  int  RTag;   //左右标志
} BiThrNode, *BiThrTree;