多路平衡归并

由公式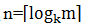可知，当初始归并段的数量m确定时，k值越大，归并的轮数n就越小，从而可以减少内外存之间磁盘读写次数。

若在进行排序时使用k-路归并排序，在k个归并段的第i个记录之间选择最小者，也就是从k个记录中选择最小者，需要进行k-1次关键字的比较。每次归并时，文件中的大部分甚至所有记录都要扫描一遍，假设文件中有u条记录，每次归并需要做(u-1) (k-1)次关键字比较；若完成一次排序需要进行n轮归并，那么在归并的过程中关键字比较的次数为：

当初始归并段的数量与文件中记录的数量一定时， (u-1)值为一个常量；(k-1)/ 在k增大时趋向于无穷大，随之归并过程中的比较次数也趋近于无穷大。因此，若一味提高k值，伴随着归并次数降低而减少的磁盘读写带来的消耗，会被内部归并增加的消耗抵消。也就是说，在k-路平衡归并中，并非k值越大越好。

那么该如何处理这一矛盾？败者树（tree of loser）可以解决这一问题。败者树是树形选择排序的一种变形，与树形选择排序不同的是，在败者树中，父结点记录孩子结点之间关键字较大的记录（即败者）对应的段号，而将关键字较小记录（胜者）的段号往上层传递，使之继续参与比较，找到最终的胜者（所有叶子结点中关键字最小的记录）。

假设使用5-路归并排序，现在有5个初始归并段F0~F4，归并段中的每条记录对应的关键字分别如图1所示：

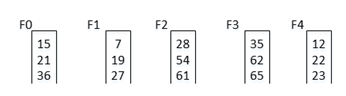
图1 初始归并段F0~F4

对这5个归并段进行5-路平衡归并的步骤如下：

（1）构建败者树。败者树是一棵完全二叉树，其中的叶子结点为本次需要进行归并排序的数据，因为进行5-路归并，所以初始败者树是一棵有5个叶子结点的完全二叉树。树的根节点为本轮比较的败者。为了记录比赛的结果，需要再添加一个结点记录本轮比赛的胜利者。综上，初始败者树如图2所示。树中每个非叶子结点中的“5”代表初始化结点数据为段号5，5号归并段F5中只有一个段结束标志，是一个空段，其中的关键字记为 。

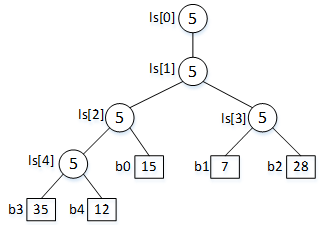
图2 初始败者树

（2）进行比较，为树中各结点赋值，理论上是从最后一个叶子结点开始比较，逐个向前使之与双亲结点作比较，但是因为叶子结点的双亲结点值最终总是子结点中的败者，所以下面阐述的过程中使子结点比较后直接赋值。

a) 结合图9-58，首先比较b3和b4，b3>b4，b4胜b3负，修改其父结点ls[4]的值为3，将胜者b4往上传递；

b) 其次比较b4和b0，b4胜b0负，修改父结点ls[2]的值为0，将胜者b4继续上传；

c) 然后比较b1和b2，b1胜b2负，修改父结点ls[3]的值为2，将胜者b1往上传递；

d) 最后比较b4和b1，b1胜b4负，修改父结点，也就是根节点ls[1]的值为4，并修改结点ls[0]的值为1，使其记录最终的胜者b1。

至此败者树构造完毕，构造过程中败者树的变化状况如图3中(a)~(d)所示。

图3 败者树赋值变化过程

（3）将胜者ls[0]对应的记录写到输出归并段，若对应的归并段F1不为空，则在其对应的叶子节点b1处从归并段F1中补充一条记录（第一次补充的为F1中的第二条记录19），从补充的叶子结点处向上开始，根据败者树的规则进行调整；若归并段F1为空，则补充一个关键字足够大的虚记录（如∞）。

（4）若胜者ls[0]中记录的关键字等于虚记录 ，则归并结束，这k个初始归并段被归并为1个归并段；否则继续执行步骤(3)。

当图9-59中的步骤执行完毕之后，b1中关键字对应的记录被输出，同时从归并段F1中读取下一条记录（关键字为19）到b1中，从b1处开始往上进行调整，调整后的败者树如图4所示。

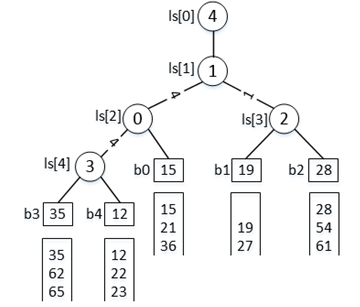
图4 第二次败者树调整结果

在使用k-路归并排序合并归并段时，重复上述步骤，直到k个初始归并段合并成一个有序序列为止。此时文件的归并时间为，与k值无关。