快速排序
快速排序(quick sort)是对冒泡排序的改进,该算法由C·A·R·Hoare在1962年提出。快速排序的基本思想是:通过一趟排序,将序列中的数据分割为两部分,其中一部分的所有数值都比另一部分的小;然后按照此种方法,对两部分数据分别进行快速排序,直到参与排序的两部分都有序为止。
使用快速排序算法进行排序时,为了将序列划分为如上所述的两部分,需要在一开始的时候设置一个参考值,通过与参考值的比较来划分数据,通常选用序列中第一个记录的键值作为参考。
对于一个包含n条记录的序列arr[],使用快速排序使序列调整为升序序列的基本操作如下:
(1)设置变量i和变量j,分别记录序列中第一条记录和最后一条(n-1)记录对应的下标,使用变量key记录序列中第一条记录的键值(为了降低学习难度,这里的键值即为一条记录),即使key=arr[0];
(2)若i<j成立,
a. 比较arr[j]和key,若key>arr[j],使arr[i]=arr[j];否则从后往前移动j,即使j--;
b. 比较arr[i]和key,若key<arr[i],使arr[j]=arr[i];否则从前往后移动i,即使i++;
(3)重复上述步骤(2),直到i<j不成立为止,此时使arr[i]=key。
经过上面的三步操作,初始序列被分为两个子序列:在参考值key所在记录之前的记录,其键值小于key;在参考值key所在记录之后的记录,其键值大于key。
完整的快速排序就是对上述三步的递归调用,当left>=right成立时,递归结束,排序完成,此时序列被调整为一个升序序列。
下面以序列arr[10]={5,0,9,8,1,4,6,3,7,5}为例,演示使用快速排序算法获得一个升序序列的过程。
初始状态下,使用key记录arr[0]的值作为本层比较中的参考值,使用i和j记录第一个元素的值和最后一个元素的下标,如图1所示。

图1 初始状态示意图
本层的key值等于arr[0],也就是5,arr[0]对应的位置可视为空值。
首先使arr[j]与key比较,因为arr[j]=key,所以使j减1;i<j,再次比较arr[j]和key,同上,j继续减1;此时j=7,i<j,arr[j]=3,arr[j]<arr[0],将arr[7]中存储的数据放到arr[i]。此时arr[j]对应的位置可视为空值。本次操作的过程如图2中①所示,操作结果如图2中②所示。

图2 第一层快速排序过程图示
然后从前往后遍历序列,直到找到一个大于key的值为止。查找过程中发现,在i<j的前提下,arr[0]=3和arr[1]=0都小于key;i继续加1,此时i=2,数据arr[2]>key,所以使arr[j]=arr[i]。此时arr[i]对应的位置可视为空值。本次操作的过程如图2中的②所示,操作结果如图2中③所示。
其次从后往前查找:使j减1,往前搜索小于key的数据,在i<j的情况下,找到当j=5时,arr[j]<key,使arr[i]=arr[j]。本次操作的过程如图2中的③所示,操作结果如图2中④所示。
之后从前往后查找:使i加1,在i<j的情况下,依次找到的第一个使arr[i]>key的值为arr[3],使arr[j]=arr[i]。本次操作的过程如图2中的④所示,操作结果如图9-7中⑤所示。
再次从后往前查找:使j减1,在i<j的情况下,依次找到的第一个使arr[j]<key的值为arr[4],使arr[i]=arr[j]。本次操作的过程如图2中的⑤所示,操作结果如图2中⑥所示。
从前往后查找:使i加1,因为此时i=j,所以本层排序结束。原始序列被数据“5”分为两个子序列。排序结果如图3所示。

图3 第一层排序结果
之后通过递归调用对两个子序列进行操作,并对子序列划分出的序列进行排序,每一层递归操作中的位置变动如下图4所示。
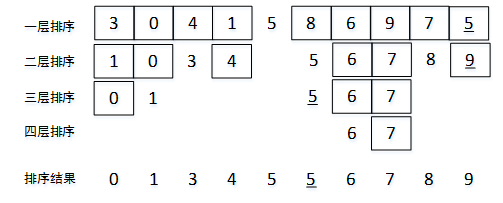
图4 快速排序全过程结果图示
学习了快速排序的基本操作步骤,下面给出算法的代码实现。
//快速排序
void QuickSort(int arr[], int left,int right)
{
if (left >= right) //如果左边索引大于或等于右边索引,说明该组序列整理完毕
{
return;
}
int i = left;
int j = right;
int key = arr[i]; //使用key来保存作为键值的数据,将arr[i]空出来
//本轮排序开始,当i=j时本轮排序结束,将键值赋给arr[i]
while (i < j)
{
while ((i < j)&&(key <= arr[j]))
{
//不符合条件,继续向前寻找
j--;
}
arr[i] = arr[j];//从后往前找到一个小于当前键值的数据arr[j],将其赋给arr[i]
//赋值之后arr[j]相当于一个空的、待赋值的空间
//从前往后找一个大于当前键值的数据
while ((i < j) && (key >= arr[i]))
{
//不符合条件,继续向后寻找
i++;
}
//找到或i<j不成立(即序列查找完毕时)while循环结束,进行赋值
arr[j] = arr[i];
}
arr[i] = key;
//递归调用排序函数对键值两边的子序列进行排序操作
QuickSort(arr, left, i - 1);
QuickSort(arr, i + 1, right);
}以上的算法实现,其核心是一个while循环,在该循环中实现下标的移动和数据的对比调整。while循环完成之后,序列被选定的参考值划分为两个子序列,然后通过递归调用函数自身对子序列进行操作。在理想情况下,每一次序列划分都划分出两个等长的序列,那么需要划分log2n次,此时快速排序的时间复杂度为O (nlog2n);而最坏情况下,原始序列已经基本有序,每次划分只能减少一个元素,此时快速排序退化为冒泡排序,时间复杂度为O(n2)。因此快速排序的平均时间复杂度为O(nlog2n)。
相比于冒泡排序,快速排序的排序效率有了质的飞跃,并且快速排序在排序的过程中只需要常数级的辅助空间,空间复杂度仅为O(1)。当然使用递归算法时,每次递归调用需要开辟一定的栈空间,这个空间总大小为nlog2n,所以快速排序的空间复杂度实际为O(nlog2n)。因为冒泡排序存在跳跃性的位置变换,所以关键字相同的两条记录在排序之后先后次序可能发生改变,这个算法是一个不稳定的排序算法。
